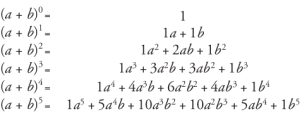Patterns make it easier to calculate or find values. A pattern is generally something that we can memorize because it  always works the same way. If there is the number 11 multiplied by 2, we get 22. The same number multiplied by 3 gives us 33.  That  pattern that stays the same for all numbers from 1 to 9 mulitplied with 11, so since we know that, whenever we have to multiply the number 11 we remember that pattern and don´t have to do all the math in our head, which saves work and time. Just when 11 is multiplied with number higher than 9, the pattern changes. There is still a pattern, it just changes a little bit.

Patterns also help us to deal with Binomials, since the way and order we solve them are always the same, even if the numbers are different. There are three different kinds of binomials, so the patterns make it way easier to solve them is less time and more efficiently once we know what kinds of binomials there are and how to use the patterns on them.

To make those patterns more visual, we use algebra tiles in which we can see how the factors relate to each other in a rectangle.

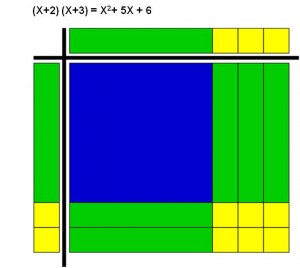
This is a really good example of an algebra tile, using the equation (x+2)(x+3). x+2 and x+3 are the sides of the rectangle, so in the diagram the sides are composed of at least 2 parts, one of which is the x, that is equal on both sides and is colored in green. Then there is the amount of smaller squares, according to how often the variable x is in the formula, in this case it is 2 and 3, which are colored in yellow. Now we extend those  lines into the rectangle, so we get many little fields inside the rectangle that represent the product of the sides. The big blue box is x^2, the smaller green fields add up to 5x and the small yellow fields represent 2*3, which is 6. If we draw the diagram properly, the amount of fields inside the rectangle will be equal to the numbers on the outside, so then we just need to count them, add them to one equation and that takes a little more time, but it prevents mistakes.

But also without algebra tiles there are patterns that help us to solve not only binomials, but almost for every kind of equation there are certain similarities that allow us to find patterns. The best example for this is again binomials because there the ways we solve them never change, as long as we memorize the patterns and pay attention to positive and negative values.

In example a in the picture we see the binomial (x+3)(x+5), which is the first of the three binomials and the easiest one, because it has all positive values and we don’t have to worry about making mistakes there. No what we do is we multiply all the terms inside both brackets with each other, so here are all the multiplications happening in the binomial (x+3)(x+5):

x*x

x*3

x*5

3*5

which gives us

x^2 + 3x+5x + 15

which can be summarized to

x^2 + 8x+ 15

This way of solving type 1 binomials will never change, even if there is (x+100)(x+37), or any other values, which will eventually make it more difficult as the numbers get bigger.

Now the second and third type of binomials are different, because they have positive and negative values in them. The second type is the most difficult one because there is a negative value in both brackets so there might be mistakes happening. The third type, where one bracket is all positive and the other one has a negative value has the most significant pattern of the three:

(x+3)(x-3)

which gives us

x^2 – 9

because +3x-3x cancel each other out and that leaves us x^2 -9.

This pattern will only work as long as the number values in the brackets are the same, it would not work in for example:

(x+3)(x-2)

Here they do subtract each other but it leaves 1x because one number is bigger than the other

Binomials is always about multiplying brackets. For the pattern that I described in this post it does not matter how often we do that. If it is only twice, or five times that we multiply the bracket with itself, does´t change the pattern, it may just look a little bit more complicated because the equation gets longer, but we still distribute all the factors with each other.

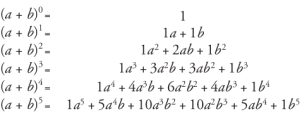
Those were only a few examples of patterns in math, but there is a lot more that we either commonly use or haven´t learned yet, and also some people have different patterns that they find convenient for themselves, so we do by far not know all of them yet. The ones that we do know save us a lot of time and work and prevent mistakes which is why we pay attention to them in math class.