1.Representing repeated multiplication with exponents-multiplication is the same thing as repeated addition. And exponents are the same thing as repeated multiplication.
Ex. x+x+x=
x is the base and 3 is the exponent or how many times x is multiplied by itself .
2.Discribe how powers represent repeated multiplication- powers represent repeated multiplication because you don’t multiply the exponent by the base, you multiply the base with itself, depending on what number the exponent is.
Ex. =
3.Demonstrate the difference between two given powers in which the exponent and the base are interchanged by building models of a given power. The first model is because there are 3 edges that equal 2. the second model is
because the length is 3 and the width is 3.
4. Demonstrate the difference between two given powers in which the exponent and the base are interchanged by using repeated multiplication
It is the difference between and
the answer is different because when you put
, it equals
, but when you write
, it equals
5.Evaluate powers with intergral bases (excluding base 0) and whole number exponents.
=9
=4
=1
=1
=4
=9
6.Explain the role of parentheses in powers by evaluating a given set of powers.
is the same thing as
because it all equals to
. But,
is equal to
7. Explain the exponent laws for multiplying and dividing powers with the same base.
Product law: 1. Keep the base 2. add the exponents 3. multiply the coefficients
Ex. = Keeping the 4 as 4. Adding the exponents (2+3=5). and multiplying the coefficients. (3×2) so you end up with
Quotient Law: 1.Keep the base 2. divide coefficients 3. subtract exponents
You just subtract the exponents so then it equals 5.
8.Power law=1. Keep the base 2. multiply the exponents 3. don’t forget you coefficants.
Multiply
=
9. Explain the law for powers with an exponent of 0.
Any base to the power of 0=1, with the exception of 0 as a base, which is undefined.
=1
=1
=1
10.Use patterns the show that a power with an exponent of zero is equal to one.
=8
=4
=2
=1
As the exponents decrease by one, the answer is divided by the base.
11.Explain the law for powers with negative exponents
- Reciprocal the base(flip) 2. make exponent positive(because of the flip)
↓ ↓ ↓
=4+16
↓ ↓
=20
↓
In line 2, the problem was that addition and subtraction was done before division
Correct solution
↓ ↓ ↓
=4+16
↓
=4+8-4
↓
=12-4
As you can see, messing up 1 step effects your whole equation.
18. Use powers to solve problems (measurement problems)
Find the surface area of the blue shaded square
=25-9
=16
19.Use powers to solve problems (growth problems)
Your making dough with (magic) yeast in it. every hour, the weight of the dough doubles. The dough weighs 1.2lbs. at the start. What happens to the weight of the dough after
2 hours=1.2∙2=2.4lbs.
2.5 hours=1.2∙2.5=3lbs.
3 hours=1.2∙3=2.6lbs
x hours=1.2∙x=1.2xlbs.
Example, In Science class the students made expanding elephant toothpaste and every 10 minutes the size of the goo doubled. They started out with 5ml of toothpaste, how much toothpaste was there after…
A) 10 minutes: = 10ml
B) 30 minutes: = 40ml
C) 1 hour: = 320ml
x hours:
20.Applying the order of operations on expressions with powers involving negative exponents and variable bases.
Don’t skip any steps when you have negative exponents. and keep track of your exponents.
Power: An expression made up of a base and a power
Base: the number you multiply itself by in a power
Coefficient: Number in front of the variable
Exponent: the number of times you multiply a base in a power
Exponential Form: A short way to write repeated multiplication
Pythagorean Theorem:
Squared: To the power of 2
Cubed: To the power of 3
Multiplication is repeated addition, and exponents are repeated multiplication.




1. I like how you explained that repeated addition is the same as multiplication, and that repeated multiplication is the same as exponents, however in you example of repeated multiplication you used x as the base, but you ADDED x+x+x in stead of multiplied (x)(x)(x).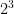 as 2x2x2 because volume is (length)(width)(height)
as 2x2x2 because volume is (length)(width)(height)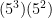 where you just add the 3+2 and get
where you just add the 3+2 and get  And it doesn’t involve multiplying a coefficient
And it doesn’t involve multiplying a coefficient = 5 but you could’ve explained that anything to the power of 1, the base stays the same.
= 5 but you could’ve explained that anything to the power of 1, the base stays the same.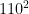 =
= 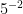 and
and 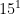 =
= 
2. Good job, i understand what you saying but the latex coding that you used resulted in “5times5times5times5” you don’t need coding to write 5x5x5x5
3. Yes but you could’ve included the formula in
4. Well explained, although it’s written as 3times3times3 again.. not that there’s anything wrong with it, it just could be neater
5. Maybe explain the rule for a negative base (a negative base to the power of an even number will always be positive. A negative base to the power to an odd number will always be negative)
6. Yes 🙂
7. Product law, yes. I like how you made the question including the coefficient, some people (including me) made the equation alot easier ex. As
Quotient law, you said “you just subtract the exponents so it equals 5” you had the exponents as 6 and 5 so yes 6-5=1 and
8. yesss, you woul multiply the exponents and keep the base
9. Why does anything to the power of 0 equal 1 though?
10. Well explained
11. Explanation could be more detailed, what if i don’t know what reciprocal means? Where does the postive exponent now go, by the denominator or the numerator?
12. Frac? Explain why
13. Yes
14. Well explained
15. It’s a little hard to read this equation but it is correctly explained
16. Good job
17. I like how you explained that one error changes the whole answer
18. Explain why you subtract the two surface areas
19. Well explained. I liked that you gave an example of an “x” amount of hours, it shows that the pattern continues
20. Goog job. You solved it correctly. I like that you highlighted the negative exponents to show their negative
Great job on this assignment, I can tell you worked hard on it. 🙂
-By Brenda/mom