Week 15- Pre calc 11

December 21, 2017 katelynw2015

Week 15 of pre calc 11 included a lot of fractions and aria keys. This week we learnt how to multiply and divide rational equations. When multiply and dividing there are 3 steps that I always follow.

1. Factor

2. Cross out copies

3. Rewrite the equation and simplify if possible

Lin order to find non permissible values you need to look back into the equation a and find all the factored forms with M. In this example m/=/ -3,2-2, and 0. Whenever m has acosfficient, in the example 3, then the non permissible value of m is always going to equal 0

Week 14- Pre calc 11

December 11, 2017 katelynw2015

This week we had review for our Graphing absolute values and reciprocals test, and then we did the test once Thursday. We also did our first lesson for the new unit we are starting which is, rational expressions and equations.

We already know that a rational number is a quotient of 2 integers. That means that the quotent of 2 polynomials is called a rational expression.

This example shows how the value of x changes the equation. It also shows that each value is the same for the 2 rational expressions

Week 13_ pre calc 11

December 7, 2017 katelynw2015

this week in pre cal 11, I learned how to graph absolute values. We already know that when you have an absolute value it can’t be negative, the same goes for when you are graphing it, the graph can’t go into the negative section. This means that when you graph a line you have to take the part that is INV the negative area and reflect it up so its positive.

In this example you can see that the dotted line is the part of the graph that would have continued into the negative area. Instead of it going negative the line was reflected into the positive area to make a V shape.

Week 12- Pre Calc 11

November 28, 2017 katelynw2015

In week 12 we did a lesson on solving Quadratoc systems of equations. Just by looking at the graph we can tell how many solution it will have.

In order to solve quadratic systems of equations you need to use substitution.

Ex:

x-2y=-10

3x-y=0

isolate one of the variables

3x=y

put 3x into y

x-2(3x)=-10

x-6x=-10

-5x=-10

x=2

put ^ (x=2) back into the equation to find y

2-2y=-10

-2y=-12

y=6

answer: (2,6)

Week 11- Pre Calc 11

November 28, 2017 katelynw2015

This week we started looking at solving Quadratic Inequalities in 1 variable.

In order to solve quadratic inequalities we need to find the zeroes of the functions. To find the zeroes of a function we need to factor.

For example; $x^2+2x-8>0$

we can factor that into; (x+4)(x-2)>0

the zeroes of the function are; -4 and 2

from finding the zeroes of the function we can determine what numbers x can be to make it positive or negative.

To find if what x needs to be, you place both the zeroes of the function on a number,one and substitute a number in x three time. One needs to be less than -4 (lowest zero pair) another one needs to Ben more than 2 (greatest zero pair) and he third numbers needs to be in between -4 and 2. By solving the equations we can figure out what x has to be greater than and less than.

In this case the solution for the inequality is; x<-4 and x>2

Week 10- Pre Calc 11

November 23, 2017November 23, 2017 katelynw2015

This week we did the Mid-term. Leading up to the midterm I did a lot of review. We did the review in class where our groups made our own questions and put the, all into one big review where we solved everyone else’s questions as well. I did all the questions that were on that review page. I also went onto the Pre calc 11website where our textbooks are from and I downloaded that review and completed it as well. Mr. Cornwall also helped me lots after school on Thursday with a bunch of questions that I had. I went to him because he taught me for part of last year and he knows how I learn best so he helped me understand some concepts that weren’t making sense to me before. Some of my friends including; Molly, Chris, JP, and Quinn went to Mr.Chee’s room and used the white board to work together to figure out problems that we didn’t understand. I worked hard over the long weekend with my brother who also help me study. This is some of the most studying I have ever done for a midterm and I really hope it pays off.

Week 8- Pre Calc 11

November 6, 2017November 6, 2017 katelynw2015

For week 8 in Pre-calc 11 we learned to analize Standard form (vertex form). In my opinion this is the easiest form to graph becasue you are already given the vertexand with it you can find the x and y intercepts, the line of symmetry, and the domain and range. Each number in the standard form tells you something different about how it needs to be graphed.

Standard form: $y=a(x-p)^2+q$

a- determins the width of the graph. If a<1 then the graph will become wider and if a>1 then the graph will become thinner. A also determines if the graph will be opening up or down. If a is positive then the graph will open up, but if it is negative then it will open down.

p- determins the horizontal translation of the graph. If p is positive then the graph will slide left to the negative side. If p is negative then the graph will slide right to the postivive side. Basically you do the opposite of what p really is, so if you have p=-2 then you go +2 along the x axis.

q- determins the vertical translation of the graph. If q is negative then you slide the graph down the y axis into the negative side. If q is a positive then you slide the graph up the y axis into the positive side

This form is also known as vertex form because it gives you the vertex, which will we (p,q)

Example: $y=3(x-2)^2+1$

Just by looking at this I can tell that the graph is going to be skinnier, move 2 to the left (positive) and will also go up one along the y-axis.

There is no x-intercepts because y>1 and the graph is opening up which means the graph will not touch the x-axis

Week 7- Pre Calc 11

November 6, 2017 katelynw2015

In week 7 we started looking over properties of a quadratic function. In this lesson we determined the characteristics of a quadratic function and how to solve it.

We determined if a table of values represented a quadratic function. You could tell this by seeing how much y went up.

Example: 5,0,-7,-16,-27

to get from 5-0 you -5, to get from 0–7 you -7, and to get from -7–16 you -9. The pattern here is you are adding 2 to how much you subtract each time

A few of the first things I learned include; finding the vertex, the x and y intercepts, the line of symmetry, and the domain and range.

Example: $2x^2+8x+6$

Vertex: (-2,2)

x-intercepts: (-3,-1)

y-intercept: (6)

Line of symmetry (-2)

Domain: (XER)

Range: (y>-2)

Week 6-Pre Calc 11

October 18, 2017 katelynw2015

This week in Pre Calc 11we learned the 3 ways to solve quadratic equations. The 3 ways are;

1. Factoring

2. Completing the squares

3. Using quadratic equation

Factoring: this is the easiest way to solve quadratic equations

Example:

$x^2-9x-22=0$ > Start off with your equation

$x^2-11x+2x-22=0$ > find your 2 numbers that multiply to 22 and add to -9 (-11,2)

$(x-11)(x+2)$ > factor by grouping common term (look at week 5 post)

$x=11 x=-2$ > when you have your 2 bracketsyou take the opposite of both numbers and those would be what x equals, in this case the opposite of -11 is 11 and the opposite of 2 is -2

Completing the square: $(b/2)^2$

Example:

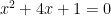$x^2+4x+1=0$ > start with your equation

$(x^2+4x+4)+1-4=0$ > separate $x^2+4x$ and +1 by using brackets, from there you take whatever number is b (4), divide it by 2 and then square it. For this equation our number will be 4, you then put that number beside 4x and you also put the opposite of that number (-4) and put it beside 1

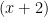$(x+2)^2-3=0$ > you foil what’s in the bracket and take the copy bracket turn it into $(x+2)$ which is the same as (x+2)(x+2). You also solve outside the bracket so 1-4=-3

$\sqrt{(x+2)^2}=\sqrt{3}> you move -3 to the other side of the = sign by makeing it 3 and the � you’ve squareboth$ latex (x+2)^2$ and 3

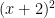$x+2=\sqrt{3}$ > by squaring $(x+2)^2$ it just becomes x+2

$x=-2\sqrt{3}$ > you then isolate x so you need to move 2 to the other side by making it -2

Week 5- Pre Calc 11

October 18, 2017 katelynw2015

This week we started a brand new unit, Factoring polynomials. I’m very happy we stared this unit because this was one of my favourite units to do last year in math 10. We spent t most of the day on Friday when we started the unit doing review. Once I did the first question everything came back to me. In my opinion the easiest factoring to do is when you have perfect square binomials like $x^2-100$ All you need to do is square root both numbers and put them in brackets. Example: $x^2-100$

$(x-10)(x+10)$

i got this answer because I put the square root of $x^2$ (x) at the beginning of each bracket. I then took the square root of 100 which is (10) and I put that at the end of each bracket. $x^2-100$ has a negative sign, that means that one of the 10 will be positive and the other one will be a negative becasue 10x(-10)=-100

When you are factoring trinomials like $x^2+7x+12$ This trinomial is an easy trinomial because it has $larex x^2 at the front$ In order Govett solve this trinomial you need to find 2 numbers that multiply to 12amd add to 7. In this case we would use the numbers 3 and 4 because 3×4=12 and 3+4=7. These are the steps I take to get the answer

$x^2+7x+12$ > we start with the original equation

&$atex x^2+3x+4x+12$ > we take our 2 numbers that multiply to 12 and add to 7 and we put them into our equation in replace of the 7 in order to expand

$x(x+3) 4(x+3)$ > we the night take the common factor out of each equation and put whatever is left over into brackets, in the step we should get the same numbers in both the bracket, I got (x+3)

$(x-3)(x+4)$ > the 2 brackets turn into one and you take the common factor from each equation and put them into a bracket (x+4)

Katelyn's Blog

Math 11