In week 12 we did a lesson on solving Quadratoc systems of equations. Just by looking at the graph we can tell how many solution it will have.
In order to solve quadratic systems of equations you need to use substitution.
Ex:
x-2y=-10
3x-y=0
isolate one of the variables
3x=y
put 3x into y
x-2(3x)=-10
x-6x=-10
-5x=-10
x=2
put ^ (x=2) back into the equation to find y
2-2y=-10
-2y=-12
y=6
answer: (2,6)
This week we started looking at solving Quadratic Inequalities in 1 variable.
In order to solve quadratic inequalities we need to find the zeroes of the functions. To find the zeroes of a function we need to factor.
For example;
we can factor that into; (x+4)(x-2)>0
the zeroes of the function are; -4 and 2
from finding the zeroes of the function we can determine what numbers x can be to make it positive or negative.
To find if what x needs to be, you place both the zeroes of the function on a number,one and substitute a number in x three time. One needs to be less than -4 (lowest zero pair) another one needs to Ben more than 2 (greatest zero pair) and he third numbers needs to be in between -4 and 2. By solving the equations we can figure out what x has to be greater than and less than.
In this case the solution for the inequality is; x<-4 and x>2
This week we did the Mid-term. Leading up to the midterm I did a lot of review. We did the review in class where our groups made our own questions and put the, all into one big review where we solved everyone else’s questions as well. I did all the questions that were on that review page. I also went onto the Pre calc 11website where our textbooks are from and I downloaded that review and completed it as well. Mr. Cornwall also helped me lots after school on Thursday with a bunch of questions that I had. I went to him because he taught me for part of last year and he knows how I learn best so he helped me understand some concepts that weren’t making sense to me before. Some of my friends including; Molly, Chris, JP, and Quinn went to Mr.Chee’s room and used the white board to work together to figure out problems that we didn’t understand. I worked hard over the long weekend with my brother who also help me study. This is some of the most studying I have ever done for a midterm and I really hope it pays off.
This week we did lots of review, but we also learned a new lesson on Modelling using quadratic equations. ThIs is the lesson that I struggled with the most in the unit and it’s easier to explain using pictures and numbers rather than words.
In the example we know that when x and y are added together they need to equal 24 so we made the equations x+y=24. The equation can also be represented by y=x-24. On the right side of the page we graphed out the equation to show us a visual representation of our equation. On the graph we made x=0 so we need to do the same to the written equation,
x(x-24)=y
0(0-24)=y
0+24/2=12
This means that
=12(12)
=144
For week 8 in Pre-calc 11 we learned to analize Standard form (vertex form). In my opinion this is the easiest form to graph becasue you are already given the vertexand with it you can find the x and y intercepts, the line of symmetry, and the domain and range. Each number in the standard form tells you something different about how it needs to be graphed.
Standard form: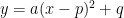
a- determins the width of the graph. If a<1 then the graph will become wider and if a>1 then the graph will become thinner. A also determines if the graph will be opening up or down. If a is positive then the graph will open up, but if it is negative then it will open down.
p- determins the horizontal translation of the graph. If p is positive then the graph will slide left to the negative side. If p is negative then the graph will slide right to the postivive side. Basically you do the opposite of what p really is, so if you have p=-2 then you go +2 along the x axis.
q- determins the vertical translation of the graph. If q is negative then you slide the graph down the y axis into the negative side. If q is a positive then you slide the graph up the y axis into the positive side
This form is also known as vertex form because it gives you the vertex, which will we (p,q)
Example:
Just by looking at this I can tell that the graph is going to be skinnier, move 2 to the left (positive) and will also go up one along the y-axis.
There is no x-intercepts because y>1 and the graph is opening up which means the graph will not touch the x-axis
In week 7 we started looking over properties of a quadratic function. In this lesson we determined the characteristics of a quadratic function and how to solve it.
We determined if a table of values represented a quadratic function. You could tell this by seeing how much y went up.
Example: 5,0,-7,-16,-27
to get from 5-0 you -5, to get from 0–7 you -7, and to get from -7–16 you -9. The pattern here is you are adding 2 to how much you subtract each time
A few of the first things I learned include; finding the vertex, the x and y intercepts, the line of symmetry, and the domain and range.
Example:
Vertex: (-2,2)
x-intercepts: (-3,-1)
y-intercept: (6)
Line of symmetry (-2)
Domain: (XER)
Range: (y>-2)
