Diagram of a power:

2. Describe how powers represent repeated multiplication
Powers represent repeated multiplication since repeated multiplication is the same as multiplying a number by itself a certain amount of times. Powers are a short way of writing out repeated multiplication for an individual number.
If you had 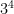 , the exponent (4) is representing the number of times the base (3) is written out in a repeated multiplication expression.
, the exponent (4) is representing the number of times the base (3) is written out in a repeated multiplication expression.
When written out in the form of repeated multiplication, 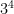 = 3
= 3  3
3  3
3  3 = 81.
3 = 81.
For example,  = 2
= 2  2
2  2
2  2
2  2 = 32.
2 = 32.

4. Demonstrate the difference between two given powers in which the exponent and the base are interchanged by using repeated multiplication, such as 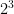 and
and 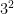 .
.
There is a difference between two given powers when the exponent and base of the powers are interchanged. Interchanging the base and exponent is not the same as switching the order of numbers in a multiplication question, and getting the same answer either way. The exponent is the amount of factors of the base you have.
For example 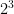 represents 2
represents 2 2
2 2 which equals 8, and
2 which equals 8, and 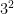 represents 3
represents 3 3 which equals 9.
3 which equals 9.

6. Explain the role of parentheses in powers by evaluating a given set of powers such as 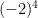 ,
, 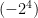 , and
, and  .
.
Parentheses have a significant role in determining whether a power will have a positive or negative outcome.
For 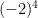 , when the negative sign is within the brackets, and the exponent is outside the brackets, it implies that the base is negative. You would apply the exponent to the negative base.
, when the negative sign is within the brackets, and the exponent is outside the brackets, it implies that the base is negative. You would apply the exponent to the negative base.
However, whenever there is an exponent inside the brackets, such as 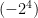 , or there isn’t any brackets at all, such as
, or there isn’t any brackets at all, such as  , the negative sign stands for a coefficient (-1) and the base is positive, so you apply the exponent to the positive base, and than the negative coefficient afterwards, since Exponents is before Multiplication in BEDMAS.
, the negative sign stands for a coefficient (-1) and the base is positive, so you apply the exponent to the positive base, and than the negative coefficient afterwards, since Exponents is before Multiplication in BEDMAS.
For example, if you have 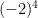 , it would be written out as:
, it would be written out as:
(-2)  (-2)
(-2)  (-2)
(-2)  (-2), which would equal +16.
(-2), which would equal +16.
If you had 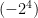 , it would be written out as:
, it would be written out as:
(-1  2
2  2
2  2
2  2), which would equal (-16).
2), which would equal (-16).
If you had  , it would be written out as:
, it would be written out as:
-1  2
2  2
2  2
2  2, which would equal -16.
2, which would equal -16.

8. Explain the exponent laws for raising a product and quotient to an exponent.
When given the expression  , people tend to use BEDMAS instead of using the raising a product to a power exponent law.
, people tend to use BEDMAS instead of using the raising a product to a power exponent law.
For example, they would multiply the numbers within the brackets first (4 x 2) = 8
Then they would apply the exponent, so they would have the expression  which equals 64.
which equals 64.
However, if you are multiplying two or more numbers inside of brackets, and on the outside of the brackets there is an exponent, you can apply that exponent to every individual number instead of applying that exponent to the product of the numbers inside the brackets. This is called raising a product to an exponent, which is an exponent law.
For example, if you have the expression  you could write it as:
you could write it as:


 which is equivalent to 16
which is equivalent to 16  4 = 64.
4 = 64.
In certain expressions, such as  , it would be easier to apply BEDMAS, however in other expressions using the raising a product to an exponent law is more efficient.
, it would be easier to apply BEDMAS, however in other expressions using the raising a product to an exponent law is more efficient.
For example, if you have the expression  instead of using BEDMAS and evaluating the expression within the brackets first,
instead of using BEDMAS and evaluating the expression within the brackets first,  =
=  =
=  , you could apply the raising a product to an exponent law,
, you could apply the raising a product to an exponent law,
 =
=  = 27
= 27 

 64 =
64 =  .
.
27 

 64 is easier to evaluate than
64 is easier to evaluate than  .
.
When given the expression  , people also tend to apply BEDMAS instead of using the raising a quotient to a power exponent law.
, people also tend to apply BEDMAS instead of using the raising a quotient to a power exponent law.
For example, they would divide the numbers within the brackets first  = 2
= 2
Then they would apply the exponent, so they would have the expression 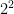 which equals 4.
which equals 4.
However, if you are dividing one number by another inside of brackets, and on the outside of the brackets there is an exponent, you can apply that exponent to each number individually rather than applying the exponent to the quotient of the two numbers inside the brackets. This is called raising a quotient to an exponent, which is also an exponent law.
For example, if you have the expression  you could write it as:
you could write it as:
 which is equivalent to
which is equivalent to  = 4.
= 4.
In certain expressions, such as  , it would be easier to apply BEDMAS, however in other expressions using the raising a quotient to an exponent law is more efficient.
, it would be easier to apply BEDMAS, however in other expressions using the raising a quotient to an exponent law is more efficient.
For example, if you have the expression  , instead of using BEDMAS and evaluating the expression within the brackets first,
, instead of using BEDMAS and evaluating the expression within the brackets first,  =
=  ≈ 1.78, you could apply the raising a quotient to an exponent law.
≈ 1.78, you could apply the raising a quotient to an exponent law.
 =
= 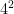

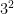 = 16
= 16  9 =
9 =  ≈ 1.78.
≈ 1.78.
64  9 is easier to evaluate than
9 is easier to evaluate than  .
.

10. Use patterns to show that a power with an exponent of zero is equal to one.
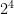 =16,
=16, 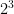 = 8,
= 8, 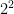 = 4,
= 4, 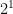 = 2, so
= 2, so 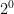 has to equal 1.
has to equal 1.
When you write out all the powers of a certain base, and find the answers for all of them, you will notice a pattern. As the exponent decreases by 1, the answer is divided once by the base. As shown above, as the exponent decreases by 1 from 5 to 4, the answer for  which is 32 is divided by 2 which is 16 since
which is 32 is divided by 2 which is 16 since 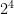 = 16.
= 16.
So if 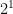 = 2, than if you decrease the exponent by 1, which would equal 0, you would have to divide the previous answer by 2.
= 2, than if you decrease the exponent by 1, which would equal 0, you would have to divide the previous answer by 2. 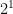 = 2, and
= 2, and  = 1.
= 1.

12. Use patterns to explain the negative exponent law.
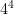 = 256,
= 256, 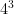 = 64,
= 64, 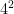 = 26,
= 26, 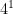 = 4,
= 4, 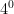 =1,
=1,  =
=  ,
,  =
=  .
.
As said above, when you write out all the powers of a certain base, as you subtract 1 from the exponent, the answer will be equivalent to dividing the previous answer by the base number.
If you take 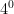 = 1, and you subtract 1 from the exponent, which would make it
= 1, and you subtract 1 from the exponent, which would make it  , to find the answer you would divide the 1 (the previous answer) by 4 (the base number) where you would get 1
, to find the answer you would divide the 1 (the previous answer) by 4 (the base number) where you would get 1  4, which is the same as
4, which is the same as  .
.
As you keep dividing by the base (which is 4) and you have negative exponents, your answer is going to be the reciprocal of what the answer would have been if the exponent was positive.
For example, 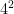 = 16 while
= 16 while  =
=  . They are the reciprocal of each other.
. They are the reciprocal of each other.

14. I can identify the error in a simplification of an expression involving powers.
A common error in the simplification of an expression using powers is when people apply the product and quotient law when trying to find the sum and difference of powers. The quotient law applies to powers when you are dividing two powers with the same base. The product law applies to powers when you are multiplying two powers with the same base. You have to apply BEDMAS when adding and subtracting powers.
A typical mistake made with the quotient law is that it is applied to a subtraction question, such as
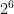 –
– 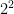 =
= 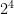 which would lead them to assume the answer is 16.
which would lead them to assume the answer is 16.
However, you cannot apply the quotient law to a subtraction question, so the solution should be written out as:
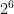 –
– 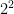 = 64 – 4 which is 60.
= 64 – 4 which is 60.
The product law applies to powers when you are multiplying two numbers with the same base. People often apply the product law in an addition question, such as 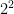 +
+ 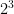 =
=  which would lead them to believe it equals 32.
which would lead them to believe it equals 32.
Although, you can’t apply the product law to an addition question, so the solution should be written out as:
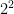 +
+ 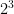 = 4 + 8 which is 12.
= 4 + 8 which is 12.

In addition, there is sometimes confusion with the power law, since the power law is when you multiply the exponent within the brackets with the exponent on the outside of the brackets. This is used so you only have to multiply the base by one exponent.
A common error is that people confuse the power law with the product law, and add the two exponents together, such as:
 =
=  which would guide them to think the answer is 256. However, the solution should be written out as
which would guide them to think the answer is 256. However, the solution should be written out as  which is
which is  which is 4096.
which is 4096.

16. Determine the sum and difference of two powers.
You can easily and quickly determine the sum and difference of two powers by evalutating the answer for each individual power, and either use addition or subtraction to answer the problem. Do not apply the product or quotient exponent law since you are adding and subtracting, and these laws only apply when you’re multiplying or dividing two powers with the same base.
For example, 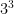 +
+ 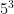 you would evaluate
you would evaluate 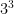 , which is 27, and then
, which is 27, and then 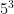 which is 125, and then you would add the two numbers together. 27 + 125 is 152.
which is 125, and then you would add the two numbers together. 27 + 125 is 152.


18. Use powers to solve problems (measurement problems)
You can use powers to solve a variety of measurement problems, one of them being to find the surface area and volume of a cube. To find the surface area of a cube you need to find the area of one side of the cube, and multiply that number by 6 (since there is 6 sides on a cube). You can find the surface area of a 5cm x 5cm x 5cm cube by using the expression
 since
since  is equal to 5cm x 5cm = the area of one side of the cube.
is equal to 5cm x 5cm = the area of one side of the cube.  =
=  . To find the volume of the cube, you would need to multiply the length, width, and the height of the cube together. You can find the volume of the cube using the expression
. To find the volume of the cube, you would need to multiply the length, width, and the height of the cube together. You can find the volume of the cube using the expression  since the length, width, and height of a 5cm x 5cm x 5cm cube is the same.
since the length, width, and height of a 5cm x 5cm x 5cm cube is the same.  =
=  .
.

You can also use powers to solve Pythagorean theorem questions, when trying to find the length of one side of a right triangle.
For example the formula for finding the hypotenuse of a right triangle is  +
+  =
=  .
.
Step 1. If we were finding the hypotenuse of a right triangle where side a = 3mm and side b = 4mm we would start out by replacing the variables in the formula with the numbers assigned to them.The equation would look like:
 +
+ 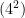 =
= 
Step 2. Then you would evaluate each individual power.  =
=  ,
,  =
=  , so the equation would look like:
, so the equation would look like:
9 + 16 =  .
.
Step 3. Next we would add the two side lengths together which would equal:
25 =  .
.
Step 4. The next step would be to find the square root of each number to isolate the c.
5mm x 5mm = 25mm so 5 is the square root of 25.
5mm= c so the missing side length (the hypotenuse) equals 5mm.
The answer is: 5mm

Another way you could use powers to solve problems is by using them to find the total volume of two shapes. As said above, you find the volume of a cube by multiplying the length, width, and height the cube together. You can find the volume a 3mm x 3mm x 3mm cube by using the power  . Then you would find the volume of the other cube, which is 2mm x 2mm x 2mm, by using the power
. Then you would find the volume of the other cube, which is 2mm x 2mm x 2mm, by using the power  . Then you would add the two volumes to evaluate the volume of the whole shape altogether.
. Then you would add the two volumes to evaluate the volume of the whole shape altogether. 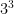 = 27mm and
= 27mm and 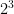 =8mm.
=8mm.  +
+  =
= 

20. Applying the order of operations on expressions with powers involving negative exponents and variable bases.
When simplifying a question that includes negative exponents and variable bases, you have to take it step by step.
I’ll be applying the steps to the expression  . Always follow BEDMAS, and make sure you evaluate powers before multiplying, dividing, adding, or subtracting, unless you are using the product or quotient law. If using the product law, it allows you to add the exponents when multiplying powers with the same base. If using the quotient law, it allows you too subtract exponents when dividing powers with the same base.
. Always follow BEDMAS, and make sure you evaluate powers before multiplying, dividing, adding, or subtracting, unless you are using the product or quotient law. If using the product law, it allows you to add the exponents when multiplying powers with the same base. If using the quotient law, it allows you too subtract exponents when dividing powers with the same base.
Step 1. Apply the product law. You add the exponent of the same base together when multiplying.

Step 2. Apply the quotient law. You subtract the exponent of the same base when dividing.

Step 3. Get rid of any negative exponents. If there is a negative exponent, you put the reciprocal of the power to make the exponent

The answer is: 

In addition, I’ll be applying the steps to the expression 
 . Always follow BEDMAS, and make sure you evaluate powers before multiplying, dividing, adding, or subtracting, unless you are using the product or quotient law. If using the product law, it allows you to add the exponents when multiplying powers with the same base. If using the quotient law, it allows you too subtract exponents when dividing powers with the same base.
. Always follow BEDMAS, and make sure you evaluate powers before multiplying, dividing, adding, or subtracting, unless you are using the product or quotient law. If using the product law, it allows you to add the exponents when multiplying powers with the same base. If using the quotient law, it allows you too subtract exponents when dividing powers with the same base.
Step 1. Apply the exponent. For this expression, we can apply the raising a product to a power law, which as said above means to apply the exponent individually to each number and variable.
 =
= 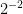


 =
= 

Step 2. Evaluate the coefficients. If there is a negative, write the reciprocal of what the answer would be if the exponent was positive.
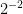 =
= 
 =
= 
Step 3. Multiply the coefficients together.


 =
= 
Step 4. Apply the product law. You add the exponent of the same base when multiplying.

(you can get rid of the 1, since any number multiplied by 1 remains the same).
= 
Step 5. Change negative exponents into positive exponents. Find the reciprocal of the number or variable if their exponent is negative.

The answer is: 



My partners Edublogs:
Kenya A: http://myriverside.sd43.bc.ca/kenyaa2019/
Nicole H: http://myriverside.sd43.bc.ca/nicoleh2019/
































