Here’s what I learned in Grade 9 fractions so far
For putting negative fractions on a number line, you have to determine the fraction’s value and put it on the number line
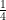

<5—-4 —3—-2—-1—-0
—3—-2—-1—-0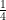 –1—-2—-3—-4—-5>
–1—-2—-3—-4—-5>
For 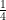 , it’s clearly less than 1, but still has a value greater than zero, so it’s placed in between
, it’s clearly less than 1, but still has a value greater than zero, so it’s placed in between
For  , since it’s a negative, it goes backwards on the number line, since if going up with positive means going on the right, negative means going on the left.
, since it’s a negative, it goes backwards on the number line, since if going up with positive means going on the right, negative means going on the left.
Comparing fractions is quite easy, it’s as simple as checking which one is bigger than the other, like this :

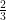
The line is clear as to which number is bigger, because 2 is clearly larger than 1. But since teachers want to test their students, you’re more likely going to find questions like these :

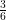
These questions aren’t as hard as you think either, all you need to do is make them equal, an easy way of doing this is by making sure both denominators are the same, and you can do this by multiplying.

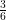
The reason why the 1 turned into 2 for the first number was because whatever happens to the denominator, happens to the numerator, it’s kind of like if 3 got caught stealing food from a grocery store, 1 would go down with them.
So now that both have equal denominators, both can easily be compared, you do this process with all fraction comparison questions that have uneven numerators and denominators.
Some numbers are a combination of a whole number and a fraction, like this :

In order to make this into an improper fraction for use, we need to multiply the denominator to the whole number, then add the result to the numerator, the end result is something like this:

One important thing to do before comparing any fraction is to make all mixed into improper first for ease of solving.
For adding and subtracting fractions, it’s just as easy, you do the same steps, but with slightly different rules.
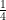 +
+
So make both of them equal like so, make sure to multiply the numerator as well:
 +
+
= 
The same applies to subtraction questions as well. But when you put a negative, that’s when the whole thing flips on it’s head
 +
+
 –
–
Both addition and subtraction can catch you off guard if you’re not careful, if it’s an addition question like this, then do a little game that goes like this :
There are two nations, Positive and Negative, they are currently fighting a war of attrition, and every group of reinforcements can be decisive to winning a battle, there are multiple ways clever field commanders can strategize, some skirmishes can go like this:
Battle 1:
-6 negative soldiers vs. 3 positive soldiers
Whatever side is larger wins the battle, so the aftermath will look like this
-3 negative soldiers surviving
This is how some battles will play out, either side must win through sheer force of manpower. Another way the battle could play out is like this:
Battle 2
-8 negative infantry units vs. 7 positive infantry units
Since this is a subtraction question, or as commanders like to call a propaganda attack, all 7 positive units defect and aid the negative side:
-15 negative soldiers
This causes the Positive nation’s defenses to be overrun, if a subtraction question has a negative on the left side, then any positive must turn into a negative as well, negative + negative = negative.
Either nation would keep fighting, one may win the battle, but not the war, so the fight between Positive and Negative will continue until the end of time.
Multiplication and Division
All you have to do for Multiplication is direct and easy, just multiply straight across

= 
And you’re done.
For Division, there are multiple ways you can go about dividing, but I’d say you should just use the Reciprocal method :

Just flip the right fraction on it’s head then multiply

= 

