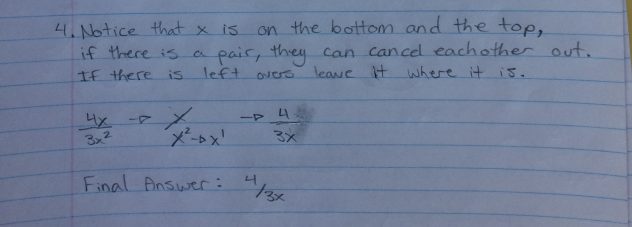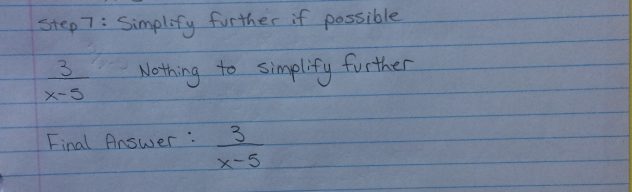Nonpermissiblevalues | Jessica's Blog

Last week in Pre-Calculus 11 we learned about multiplying and dividing rational expressions. A thing to remember about expressions is that it does not have an equal sign and you do not need to solve, you only need to simplify. I will be teaching you what non-permissible values are and how to determine what they are.

Non-permissible value : Values that cause the fraction to have a denominator with a value of zero. (In math, we cannot divide by zero).

Here is an example of multiplying rational expressions

Steps:

Step 1: Simplify $\frac{3x}{2(x-3)}\cdot\frac{8(x-3)}{9x^2}$

Non permissible values: $x\neq -3$

$\frac{3x}{2(x-3)}\cdot\frac{8(x-3)}{9x^2}$
remove (x-3) from top and bottom because they cancel eachother out
then it becomes… $\frac {3x}{2}\cdot\frac{8}{9x^2}$

Step 2: Simplify by multiplying across (Just do it)

$\frac {3x}{2}\cdot\frac{8}{9x^2}$
$\frac{24x}{18x^2}$

Step 3: Take the highest common factor from both the numerator and the denominator.

In this case 6 is the highest number that goes into both.

$\frac{24x}{18x^2}$
$\frac{4x}{18x^2}$

Step 4: Notice that x is on the bottom and the top, if it has a pair it can cancel out. two x’s on the bottom one on the top. when they cancel out each other you will be left with only 1 on the bottom.

$\frac{4x}{3x^2}$
$\frac{4}{3x}$

Final Answer: $\frac{4}{3x}$

Dividing Rational Expressions

There are many steps when dividing rational expressions

Simplify the fraction: can factor or take out the common denominator.
State the non permissible values.
Reciprocate the second fraction and it will because a multiplication expression.
State the restrictions again because there are new values in the denominator and could be non-permissible.
Simplify (cancel out like terms that have a pair on the numerator and denominator.
Multiply across (Just do it)
Simplify again if possible.

Step 1: Simplify $\frac{x+5}{x-4}\div\frac{x^2 - 25}{3x-12}$