Prescribed Learning Outcomes for Exponents:
1) Represent repeated multiplication with exponents
This wants you to show repeated multiplication, but using exponents. For example, 5x5x5x5, is the same thing as  . 5 being the base, and 4 is the exponent. Another example is 2x2x2, which is the same thing as
. 5 being the base, and 4 is the exponent. Another example is 2x2x2, which is the same thing as 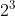 . The number 2, is the base, and then how many 2’s there are, is the exponent.
. The number 2, is the base, and then how many 2’s there are, is the exponent.
2) Describe how powers represent repeated multiplication
Powers can represent repeated multiplication. If you had, for example  , it can be also written as repeated multiplication 7x7x7x7x7. Because you have five sevens.
, it can be also written as repeated multiplication 7x7x7x7x7. Because you have five sevens.
3) Demonstrate the difference between the exponent and the base by building models of a given power, such as 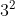 and
and 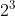 .
.
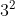 , is 3 to the power of 2, or 3 squared. And if written as repeated multiplication it would be 3×3.
, is 3 to the power of 2, or 3 squared. And if written as repeated multiplication it would be 3×3. 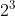 would be 2 cubed, or 2x2x2.
would be 2 cubed, or 2x2x2.

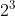 is a cube with a width, length, and height of 2. If it was cut into cubes and you count it up, it would be 8, or you can do length times width times height.
is a cube with a width, length, and height of 2. If it was cut into cubes and you count it up, it would be 8, or you can do length times width times height. 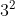 is a square with a length and height of 3. And if you count that up, it would be 9.
is a square with a length and height of 3. And if you count that up, it would be 9.
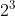 = 8
= 8
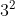 = 9
= 9
4) Demonstrate the difference between two given powers in which the exponent and the base are interchanged by using repeated multiplication, such as 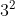 and
and 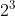 .
.
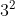 and
and 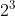 are not the same. Just because you change where the exponent and base is, the value will be different, in most cases.
are not the same. Just because you change where the exponent and base is, the value will be different, in most cases. 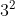 is 3×3=9, and
is 3×3=9, and 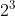 is 2x2x2=8.
is 2x2x2=8.
5) Evaluate powers with integral bases (excluding base 0) and whole number exponents.
Here is a bunch of examples on bases and powers. This question is basically asking you to solve the powers with number bases and exponents. The bases could be even or negative, and this is what happens.
 = 0x0 = 0
= 0x0 = 0
 = 1x1x1 = 1
= 1x1x1 = 1
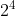 = 2x2x2x2 = 16
= 2x2x2x2 = 16
 = 3x3x3x3x3 = 243
= 3x3x3x3x3 = 243
Even bases and even exponents make even answers.
 = (-3x-3x-3)= -27
= (-3x-3x-3)= -27
If the base is negative, and the exponent is odd, then its a negative answer.
6) Explain the role of parentheses in powers by evaluating a given set of powers such as  .
.
Brackets can make the powers different. Here is what it really means of where the brackets are.
 = (-2)x(-2)x(-2)x(-2) = 16
= (-2)x(-2)x(-2)x(-2) = 16
 = (-1x2x2x2x2) = -16
= (-1x2x2x2x2) = -16
 = -1x2x2x2x2= -16
= -1x2x2x2x2= -16
If the exponent is outside the brackets, like  then that means its (-2)x(-2)x(-2)x(-2) and it equals positive 16 because an even number of negatives equals a positive. For
then that means its (-2)x(-2)x(-2)x(-2) and it equals positive 16 because an even number of negatives equals a positive. For  and
and  , the – sign is the coefficient, which makes it -1 then 2x2x2x2 which equals -16.
, the – sign is the coefficient, which makes it -1 then 2x2x2x2 which equals -16.
7) Explain the exponent laws for multiplying and dividing powers with the same base.
Whenever you have powers with the same base, then you can use either multiplying or dividing exponent laws.
For example,  , is y to the power of 3, times y to the power of 2. Instead of figuring that out then multiplying them, or if you don’t know what y is, you can also add the exponents.
, is y to the power of 3, times y to the power of 2. Instead of figuring that out then multiplying them, or if you don’t know what y is, you can also add the exponents.  which would then equal
which would then equal  .
.
The dividing one is almost the same. Except you would subtract the exponents instead. So  would be the same as
would be the same as  which is
which is 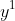
8) Explain the exponent laws for raising a product and quotient to an exponent.
This might sound confusing, but once you learn it it won’t be. Raising a product to an exponent is like  . Which then you can use the power rule. You can write
. Which then you can use the power rule. You can write  like
like  , so you just want to multiply the 2 to the ones. So it then becomes (
, so you just want to multiply the 2 to the ones. So it then becomes ( ). Another example can be
). Another example can be  . The coefficient, 2, you just bring it to the power of 3 so its 8, and then the a is
. The coefficient, 2, you just bring it to the power of 3 so its 8, and then the a is 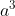 . And when you write it together it’s (
. And when you write it together it’s ( ), because you don’t know what ‘a’ is.
), because you don’t know what ‘a’ is.
The quotient rule, is also like that, in a way. So if you have the exponent 3 of the fraction is saying that it is
the exponent 3 of the fraction is saying that it is  so it can be written as 2 cubed divided by 3 cubed which equals 8 over 27.
so it can be written as 2 cubed divided by 3 cubed which equals 8 over 27.
9) Explain the law for powers with an exponent of zero.
If the exponent of a power is zero (0), then the number is just one. What I mean is, if you ever get a power the exponent is 0, for example  , then its just 1.
, then its just 1.
10) Use patterns to show that a power with an exponent of zero is equal to one.
So you know that  equals 1, or anything with an exponent of 0 also equals 1.
equals 1, or anything with an exponent of 0 also equals 1.
But why? Well, so you know that  is
is  . So when its
. So when its  ,
,  . And
. And  equals 1, because 1 times
equals 1, because 1 times  equals
equals  .
.
11) Explain the law for powers with negative exponents.
When you have a negative exponents, its a little different. You just flip the whole thing around. For example,  then equals
then equals  . Another example is
. Another example is  ,=
,=  .
.
12) Use patterns to explain the negative exponent law.
Divide by 2
23 = 8
22 = 4
21 = 2
20 = 1
2−1 = 1/2
2−2 = 1/4
2−3 = 1/8
If the base is something else, then divide it by that. Like if the base is 3 then divide it by 3 each time when your going down.
13) I can apply the exponent laws to powers with both integral and variable bases.
Integral, is like 1, 2, 3, 4, etc. and variable is like  Variable is when you don’t know what the number is or the number can change. The laws for both of them are the same except the integral you can solve it.
Variable is when you don’t know what the number is or the number can change. The laws for both of them are the same except the integral you can solve it.
 is, you know,
is, you know,  which equals
which equals 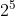 = 2x2x2x2x2 = 32
= 2x2x2x2x2 = 32
 is
is  =
=  = (
= (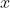 )(
)(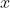 )(
)(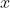 )(
)(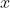 )(
)(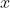 ) but since
) but since 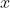 is a variable you can’t solve it. So the answer would just be left as
is a variable you can’t solve it. So the answer would just be left as  .
.
The same for the other exponent laws as well.
14) I can identify the error in a simplification of an expression involving powers.
If you get something like 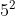 x
x 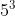 =
=  , then you know its wrong. Because your not suppose to do it like that. You can use exponent laws
, then you know its wrong. Because your not suppose to do it like that. You can use exponent laws  .
.
Or I know that  does not equal
does not equal  because the 7 under the
because the 7 under the  is actually a
is actually a  and
and  .
.
15) Use the order of operations on expressions with powers.
Using order of operations on expressions, with powers is to use the right operation first. If you get one for example,  . Instead of turning over the whole thing because of the -2 exponent outside of the brackets, you can use the power law. Then it becomes.
. Instead of turning over the whole thing because of the -2 exponent outside of the brackets, you can use the power law. Then it becomes.  After that you can use the negative exponent rule.
After that you can use the negative exponent rule.  . And when you solve it, it becomes
. And when you solve it, it becomes  . You might ask, wait what happened to the c? Well, since its
. You might ask, wait what happened to the c? Well, since its  the 0 times anything will still be 0, and then when an exponent is 0 the whole thing becomes 1. And 1 times anything is the same thing. So you don’t have to write it.
the 0 times anything will still be 0, and then when an exponent is 0 the whole thing becomes 1. And 1 times anything is the same thing. So you don’t have to write it.
16) Determine the sum and difference of two powers.
You can’t use the exponent laws when there is + or -. So you will just have to do the exponent, then add the sum/difference. For example,  , it’s 9+8=17.
, it’s 9+8=17.
And  is 9 – 8 = 1.
is 9 – 8 = 1.
17) Identify the error in applying the order of operations in an incorrect solution.
If someone does  then I know its wrong because you cannot use exponent laws for addition. You must do 9+27 which the correct answer is 36. Because exponents first, then addition.
then I know its wrong because you cannot use exponent laws for addition. You must do 9+27 which the correct answer is 36. Because exponents first, then addition.
18) Use powers to solve problems (measurement problems)
How can you use powers to solve word problems? (Measurement problems) Well this is how!
There is a blue square with a side length of 5cm. there is a red square overlapping the blue square, and the red square has a side length of 4cm. What is the area of the blue square is visible? If drawn out, it would look like this.
 You can use exponents to represent and solve this. To find area, its side length times side length, which in this case is 5cm, so its
You can use exponents to represent and solve this. To find area, its side length times side length, which in this case is 5cm, so its 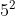 = 25. And
= 25. And  is 16. So then you do 25-16 because the 16 is covering the 25.
is 16. So then you do 25-16 because the 16 is covering the 25.
25-16=9. So the answer is  .
.
19) Use powers to solve problems (growth problems)
An example question – There once was a blob. The blob doubles every hour. How many blobs will there be by the 9th hour?
You would solve it like 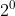 to start with. And then every hour is the exponent. 1st hour, =
to start with. And then every hour is the exponent. 1st hour, = 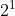 = 2. Second hour =
= 2. Second hour = 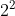 = 4. And the 9th hour would be
= 4. And the 9th hour would be  which is 512. There will be 512 blobs the 9th hour.
which is 512. There will be 512 blobs the 9th hour.
20) Applying the order of operations on expressions with powers involving negative exponents and variable bases.
Here is an example question.
 First you would make the -3 exponent, not negative. So you would flip the whole fraction around, here. After you have done that, you would then use the power law. and the final answer would be…
First you would make the -3 exponent, not negative. So you would flip the whole fraction around, here. After you have done that, you would then use the power law. and the final answer would be… 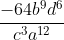


 the exponent 3 of the fraction is saying that it is
the exponent 3 of the fraction is saying that it is  You can use exponents to represent and solve this. To find area, its side length times side length, which in this case is 5cm, so its
You can use exponents to represent and solve this. To find area, its side length times side length, which in this case is 5cm, so its  First you would make the -3 exponent, not negative. So you would flip the whole fraction around, here. After you have done that, you would then use the power law. and the final answer would be…
First you would make the -3 exponent, not negative. So you would flip the whole fraction around, here. After you have done that, you would then use the power law. and the final answer would be… 





