One of the things I learned in Pre-Calc 11 on the second week is about how to add an arithmetic pattern or sequence. I find it awesome because you can know the sum of a whole sequence without adding them all together.
An arithmetic sequence is a sequence that is increased or decreased by the same amount of value.
For example, let’s say everything adds up by two(2): 3 → 5 → 7 → 9 → 11 → …
Now, that’s a sequence. What we increase or decrease by is called the common difference (d).
But how do we get the sum of these terms without adding them up together?
Before we get to that, when we add the terms of an arithmetic sequence together is called arithmetic series.
The difference when you write a sequence and a series is that:
sequence is written like this: 3, 5, 7, 9, 11,…
series is written like this: 3 + 5 + 7 + 9 + 11 + …
So how do we add them altogether? Here’s the formula:
n is how many your terms in a sequence is.
a is your first term.
is your last term.
Let’s use my previous example before as the series that we’re gonna use and let’s put the 50th term as our last term.
so it means that … 3 + 5 + 7 + 9 + 11 + …. + 101

That means that our first term is 3, our last term is 101, and the number of our terms is 50.
Plug them all in to the formula and remember: PEMDAS.
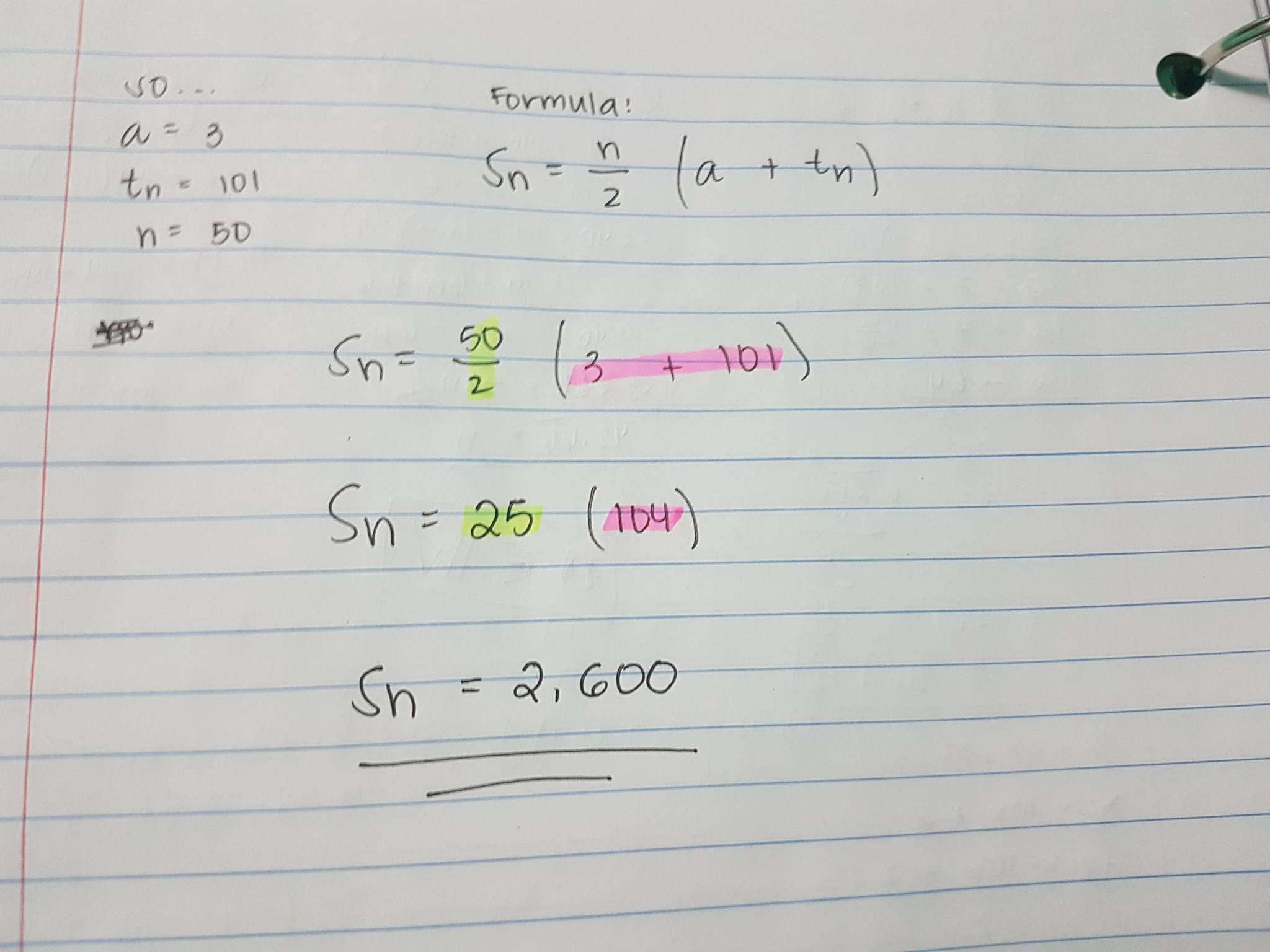
And we got it! The sum of all terms is 2,600.