Month: October 2016
Math 10 – Right Rectangular Prism (SA and V)
Right rectangular prism’s surface area and volume.
To find the surface area of a rectangular prism, all you have to do is find each side’s areas then add them all together. For surface area, the final answer must have a squared unit (n2), where the n is the unit.
The formula for it is: SA = 2(b*l) + 2(b*h) + 2(l*h)
For the volume, you just have to multiply the base, height, and length. For volume, the final answer must have a cubed unit (n3), where the n is the unit.
The formula for rectangular prism’s volume is: V = b*h*l
Base = b; Length = l; Height = h.
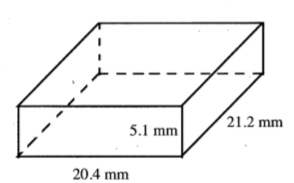
Example:
l = 21.2 mm
h = 5.1 mm
SA = 2(20.4 * 21.2) + 2(20.4 * 5.1) + 2(21.2 * 5.1) = 1289.33 mm2
V = (20.4)(21.2)(5.1) = 2205.6 mm3
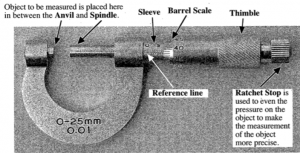
Math 10 – Micrometer
Using a micrometer to measure objects.
Instructions:
- Place the object you want to measure between the Anvil and the Spindle. You can adjust the space by spinning the Thimble.
- After that, look at the Sleeve and the Barrel Scale.
- The first reading, or the course reading is the value of the last fully visible line on the sleeve. The upper part of the sleeve is counts by a whole number; (1, 2, 3, 4, 5…) while the lower part of the sleeve is just 0.5.
- Now, look at the reference line. The reference line is the line that’s dividing the sleeve to upper and lower parts. Match the reference line with the closest line on the barrel scale. That’s your second reading, which is called barrel scale reading. The barrel scale is the part near the sleeve that can be rotated. It counts by 0.01 mm. (0.01, 0.02, 0.03, 0.10, 0.23…etc).
- Now that you have the course and barrel scale reading, add them both to get your final reading.
- The two readings on the example given were
- 9.5 mm and 0.09 mm.
- 9.5mm + 0.09mm = 9.59mm.
- The two readings on the example given were
Math 10 – Scientific Notation
What I’ve learned last week on Math 10 was Scientific Notation.
Scientific Notation is another way of writing numbers that is either too small or too large to write. Scientific notation is simplified and more convenient.
Scientific notation can only be written in form: a • 10n
Whereas a is a coefficient that is greater than or equal to 1 but less than 10.
1 ≤ a < 10.
The exponent (n), represents how many times do you need to multiply the 10 so you can reach the exact value you’re looking for. The value of your exponent is based on how many your zeros is and how many decimals are added. If you already have a decimal value, you don’t add it to your exponent.
For example, you have 48 000. To get the scientific notation form of 48 000, you need to get the coefficient, and the exponent.
Coefficient = 4.8; It is 4.8 and not 48 because you need to have a greater number or equal to one but less than ten.
Exponent = 4; It is four (4) and not three (3) because you have a decimal in your coefficient.
4.8 • 104 = 48 000.
In other words, the exponent corresponds not only to the number of zeros (0’s) you have but also how many decimals are added.