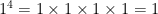1)Represent repeated multiplication with exponents:
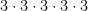 =
= 
You can count how many times the base is being multiplied by itself, and re-wright it as an exponent for how many times the base is being repeated
2)Describe how Powers represent repeated multiplication
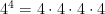
You multiply the base by itself however many times the exponent represents.
3)Demonstrate the difference between the exponent and the base by building models of a given power such as 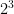 and
and 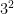
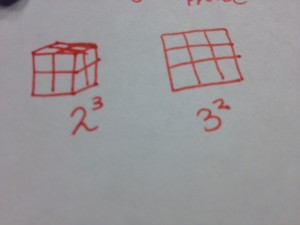
If you had a model of 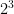 , the length of this model will be 2, the width of this model will be 2, and the Height of this model will also be 2, in a cube formation. If we had a model of
, the length of this model will be 2, the width of this model will be 2, and the Height of this model will also be 2, in a cube formation. If we had a model of 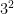 then the model would have a base of 3, and a height of 3, in a square pattern.
then the model would have a base of 3, and a height of 3, in a square pattern.
4)Demonstrate the difference between to given powers in which the exponent and the base are interchanged by using repeated multiplication
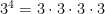 is not equal to
is not equal to 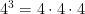
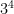 is 3 multiplied by itself 4 times.
is 3 multiplied by itself 4 times. 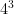 is 4 multiplied by itself 3 times. The answers are far apart and do not mean or equal the same thing.
is 4 multiplied by itself 3 times. The answers are far apart and do not mean or equal the same thing. 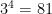 and
and 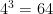
5)Evaluate powers with integral bases (excluding 0) with whole exponents
when you evaluate powers with Integral bases, and whole number exponents, you use repeated multiplication. For example:
1. 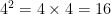
2. 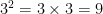
3. 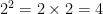
4. 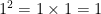
5.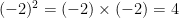
6)Explain the roll of Parenthesis in powers by evaluating a given set of powers such as, 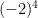
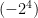 and
and 
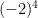 is the same as
is the same as 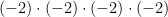 . The base of this power is(-2) and is being multiplied by itself 4 times.
. The base of this power is(-2) and is being multiplied by itself 4 times. 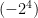 and
and  both mean the same thing. They both are equal to
both mean the same thing. They both are equal to 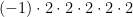 . the base is 2, and the -1 is the coefficient.
. the base is 2, and the -1 is the coefficient.
7)Explain the exponent law for multiplying powers with the same base.
When you multiply any power that has the same base, you can add the exponents together, and it will equal the same thing. for example 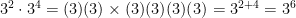
With a coefficient, you multiply the coefficient, and then add the exponents.
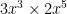
1st, 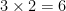 Multiply the coefficients
Multiply the coefficients
2nd 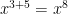 Add the exponents.
Add the exponents.
3rd 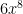
When dividing, you subtract the exponents, if they have the same base. For example 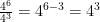
With a coefficient, you divide the coefficients, then subtract the exponents
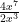
1st 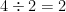 Divide the exponents
Divide the exponents
2nd 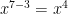
3rd 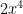
8) Explain the exponent laws for raising a product and quotient to an exponent.
When you raise a product of a quotient to an exponent, you have to use the power law. You multiply the exponents together.
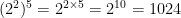
9) Explain the law for powers with an exponent of zero.
Any number besides zero raised to the power of zero will always equal one. For example, if I were to start at 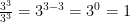 another way to explain it, is to use repeated multiplication.
another way to explain it, is to use repeated multiplication. 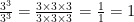
10) Use patterns to show that a power with an exponent of zero is equal to one.
1. 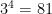
2.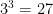
3.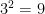
4.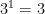
5. 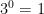
As you go down this scale, each time the answer is divided by three, so in the end, 3 divided by 3 is one, so  is one.
is one.
11. Explain the law for powers with negative exponents.
If you have a power with a negative exponent, you can turn it into a fraction using its reciprocal at the fraction, with a positive exponent.
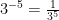
12. Use patterns to explain the negative exponent law
1.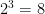
2.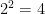
3. 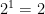
4. 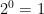
5. 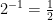
6. 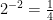
as you go down in this table, each time the quotient divides by two, so 1 divided by 2 equals 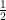
13. I can apply the exponent laws to powers with both integral and variable bases.
When you add in a variable to any exponent laws, it works the same as with any integral. 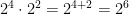 . with variables it is the same.
. with variables it is the same. 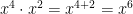
14. I can identify the error in a simplification of an expression involving powers.

15) Use the order of operations on expressions with powers.
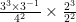
first I would simplify the exponents on the threes. 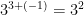 . Then I would solve for all the exponents, and that would result in
. Then I would solve for all the exponents, and that would result in 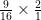 . That will equal to
. That will equal to 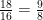
16) Determine the sum and difference of two powers.
There isn’t any laws in order to find the sum and the difference of two powers, you just have to solve for it yourself by using BEDMAS to fint the answer. 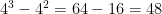 ,
, 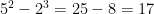
17) Identify the error in applying the order of operations in an incorrect solution.
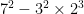 =
= ![[7-3]\times2^{2-2\times3} [7-3]\times2^{2-2\times3}](http://s0.wp.com/latex.php?latex=%5B7-3%5D%5Ctimes2%5E%7B2-2%5Ctimes3%7D&bg=ffffff&fg=000000&s=0) =
= 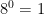
first of all, you need to follow BEDMAS when completing these problems. one of the first errors is, they multiplied all the bases together, which you are never supposed to do in any power related law. then, they added and multiplied the exponents, and did this in the wrong order according to BEDMAS. How you are supposed to answer this question correctly, is first, you evaluate all the exponents. this bring us to 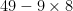 = 49 – 72 = -23.
= 49 – 72 = -23.
18) Use powers to solve problems (measurement problems)
if you had a 6 cm side length of a shaded square with another square with a side length of 4 cm of an un-shaded square inside, how mush of the shaded part is left.
To right out this question is power format, would be 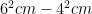 and would equal 36cm – 16cm =
and would equal 36cm – 16cm = 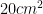
19) Use powers to solve problems (growth problems)
If my dog weighs 40 pounds as a puppy, and doubles his body weight every year, how much will he weigh by 3 years? 4 years? 6 years?
In 3 years: 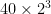 = 320
= 320
In 4 years: 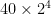 = 640
= 640
In 6 years: 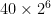 = 2560
= 2560
20) Applying the order of operations on expressions with powers involving negative exponents and variable bases.
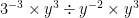
1. 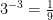
2. ![y^{3-([-2]+3)} = y^2 y^{3-([-2]+3)} = y^2](http://s0.wp.com/latex.php?latex=y%5E%7B3-%28%5B-2%5D%2B3%29%7D+%3D+y%5E2&bg=ffffff&fg=000000&s=0)
3. 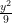
When answering these questions, you have to use BEDMAS, in the correct order. In this case, I start with Answering the exponents. with these exponents, there is still a way to simplify. I subtracted the exponents on the alike bases. Then I followed the rest in Order, remembering the negative exponents rule.
Anything else that I know about exponents…
Anything raised to the power of one, is it itself, 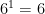
Positive 1 raised to the power of any whole number will always be 1.