Choose two different jobs that you might like to do in the next 5 years. The jobs must pay an hourly wage.
Job # 1 __Gymboree music teacher_____
Job # 2 Kitchen Design/costumer service – Woodhaven Kitchens (Dad’s work)
The hourly wage for the jobs
Job # 1 __$12.87 Job # 2 $11 .
Here are the website’s links of the jobs
http://www.gymboreeclasses.com/en/
www.woodhavenkitchens.net
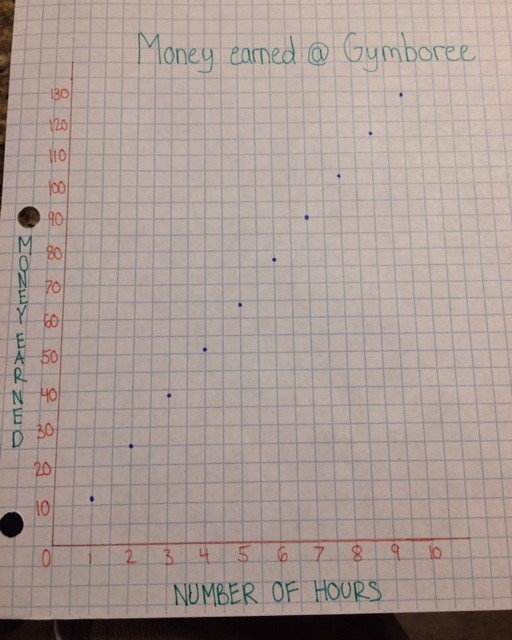
Here is a chart and a graph of each job
Job #1 – Gymboree
| Number of Hours | Total Pay |
| 0 | 0 |
| 1 | 12.90 |
| 2 | 25.80 |
| 3 | 38.70 |
| 4 | 51.60 |
| 5 | 64.50 |
| 6 | 77.40 |
| 7 | 90.30 |
| 8 | 103.20 |
| 9 | 116.10 |
| 10 | 129.00 |
| 20 | 141.90 |
| 40 | 154.80 |
| 100 | 167.70 |
| X (an unknown number of hours) | 12.90x |
Job #2 — Woodhaven Kitchens
| Number of Hours | Total Pay |
| 0 | 0 |
| 1 | 11 |
| 2 | 22 |
| 3 | 33 |
| 4 | 44 |
| 5 | 55 |
| 6 | 66 |
| 7 | 77 |
| 8 | 88 |
| 9 | 99 |
| 10 | 110 |
| 20 | 121 |
| 40 | 132 |
| 100 | 143 |
| X (an unknown number of hours) | 11x |
An equation for the hours worked and the wages earned is:
D (difference) H (hours worked) W (wages earned)
H x D = W
I would prefer to have the first job, working at Gymboree. I would prefer it because it would pay more than the other job does. Another factor to consider is the job requirements. The requirements for Gymboree are people skills, love of little kids, and some background in singing and music, all of which I have. The requirements for WoodhavenKitchens are more, such as designing and salesman skills. A third factor is training. There is very little training for Gymboree, just a couple of days to learn the routine, where as at WoodhavenKitchens I would have to learn all about the system, how to design kitchens and the different products that they use.
For the Gymboree job, I would be able to work at the most 12 hours a week, including weekends. During the week I could work a total of 6 hours. On the weekend 6 hours as well, but most of the classes they have are on weekends anyway. Say I wanted to save $1000. For every 12 hours, I would earn $154.80. In order to earn $1000 I would have to work 7 weeks in total, but it would be just over $1000, it would be $1083.6o. 6 weeks would have been to short, so 7 weeks is just right.
I had a discussion about this assignment with my parents, and we talked about many different jobs and the requirements.