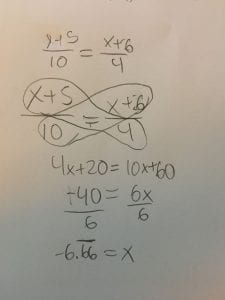Grade 11

This week in PreCalc 11 we learned how to solve rational equations where fractions with binomial or trinomial numerators or denominators are multiplied or divided by eachother or on other sides of the equal sign. There are two main ways to solve these rational equations, 1 is by cross multiplying which is done when its 2 fractions on opposite sides of the equal sign and the other is to multiply for common denominators which is usually done when there are multiple fractions on one or both sides of the equal sign.

When dividing you flip the fraction that is dividing into and change the division sign to a multiplication sign.

Example,

This week in PreCalc 11 we learned about adding and subtracting rational expressions that have binomial and trinomial denominators. So the first step in any adding or subtracting of expressions, you need to simplify the whole equation by finding common factors in the numerator or denominators.

Example,

Next we need to find a common denominator so we can add just like a normal fraction

Then you just have to simplify it further by taking the brackets out and adding/substracting respectively

2019.05.23-FR11-Jouons-un-jeu-Journal-2 (1) (1)

This week we learned about the difference between reciprocal function graph and absolute value graphs and how to graph each one.

For absolute value graphs it is graphs that reflect off the x axis/intercepts of the line to create a reflection of the parent function as in an absolute value equation we can’t get a negative, so in the graph we can’t go into the negative zone.

In a reciprocal function graph we focus on the invariant points in the parent function to create a new line that avoids the asymptotes on the x and y axis, y is usually 0 so it’s usually the x axis that we want to focus on. We use the middle of the invariant points to create the x asymptote.

Example of absolute value graph

Example of reciprocal function graph

This week we continues graphing linear/quadratic equations but this week practiced on finding the reciprocal of the equation and how it looks like when graphed.

To find the reciprocal of the equation we first have to graph the parent function, then we find our invariant points by finding the x value that corresponds with y=1 and y=-1

With these x values we can draw our hyperbolas and answer what the x value is.

Ex

.

This week we learned about graphing and solving absolute value graphs and equations, it’s similar to last chapter except with absolute value signs so the graph can’t go into the negative and is all positive. In this way it basically reflects the same way as it was going as in into the negative but in the other direction once it hits y=0.

Because of this the graphs end up looking something like this based on the type of equation (linear/quadratic)

Other than graphing we can find the x values by using previously used ways of solving for quadratic/linear equations, for quadratic specifically we’d be making one side and getting it to 0 before using the quadratic equation or factoring to get our x values.

This week we learned about graphing inequalities in two variables. It’s similar to how we did it in chapter 4, but we must find out what side of the parabola is used for the answers of the side by replacing x and y with numbers that aren’t on the line, (0,0) is the easiest to use in most cases so we usually use that to replace x and y.

In this example I show how to use this technique by replacing x and y with (0,0)

This week we learned how to do word problems with quadratic functions, like finding the maximum area of a certain amount of fencing or finding two integers with a sum or difference that have a minimum or maximum and find the answer to the maximum area or finding the two integers.

An example of how to find the integers is by taking, for example, x-y=15 and x*y=minimum and isolating one of the variables and using the substitution technique of turning it into x=y+16 and then replacing x in the multiplication with y+16 and solving before using the difference of squares to turn it into a quadratic and get an answer

Ex

.

This week in pre-calc we learned how to analyzing quadratic functions in the form of graphs using the equation

The vertex is found easily with this as the p variable is what ends up being the x value and the q variable being the y value in the vertex.

With the vertex we can then find the axis of symmetry.

With the coefficient of x (a being the variable of whatever the coefficient is) we can figure out if its maximum or minimum vertex if it’s negative or positive, if minimum it opens upward and if maximum it opens downwards. Using the information of the equation we can figure out what its congruent to as well as the rest of the information needed such as x/y intercepts and domain and range

This week I learned about the zero product law and how in a quadratic equation that = 0 we must make the x value be a opposite congruent of the other number in a factored binomial.

Basically after you have factored an equation and received an answer such as (x+2)(x+3)=0

The x value must be equal to the opposite of the number its adding to so the binomial equals 0

In that case the x would be equal to -2 so the -2 and +2 cancel out, the other x value would do the same with its binomial so it would be equal to -3 so the -3 and +3 cancel out and the equation = 0

In this example I will show how to do it from factoring to solving what x must be for it to equal 0