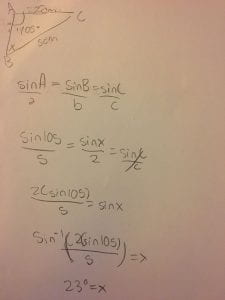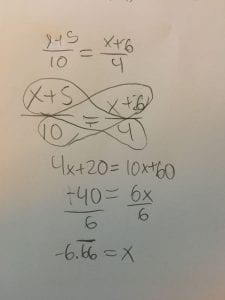Poetry in the News
Part A (thought it’d be nice to include my thinking)
It is an opinionated blog, not very serious. It is the author voicing his opinion on the subject matter of the art that is pop culture. It gets me thinking of the effect of art and pop culture on society and the world.
The subject of my poem will be the effect of art on the world and society. It will address how important types of art are in the world and how it brings out emotion because of how passionate people have become with some forms of it. It is an emotional response to how I myself feel about art, in particular movies. It will focus on the social and cultural ideologies regarding art and it’s effect. It will have an external focus of the narrator’s thoughts on art. I plan to be the narrator of the poem as the poet. I will use language that reflects how I feel about the art, it will all have it’s personal meaning, but still have it’s effect on the reader. I want to express a thoughtful and nostalgic tone, to remind everyone of their favorite art forms and make them think about how they feel about the art side of it. I will arrange the lines of my poem with 3 stanzas of 4 lines. My reader will take away from the poem a better understanding of whatever art form they love and realize how much it means to them. It will evoke nostalgia at it’s best and create an effect that leaves the reader thinking about all they love and connecting it with art. A theme of memories and attachment to art forms. My poem will celebrate the roses of the human condition, showing how we have impacted, preserved and created art, focusing on the good society has done by creating art. I will give my poem the title of “The cover of pop culture”.
Part B
 (image from http://dailynexus.com/2011-10-20/popular-culture-cultured/)
(image from http://dailynexus.com/2011-10-20/popular-culture-cultured/)
The cover of pop culture
One year, two years, three years
How long we wait for each dose of dopamine as we continue the story
We watch and we learn, appreciating the art more and more as we continue
We wait and wait, hoping to continue our adventure through the next one
From the glimpse of him as a son, the chatter from our teeth
To a glimpse of him as a father, the clap of our hands
We remember, how it ends as we learn how it starts
It’s brought together, as we cheer it on everyday through our passion
It starts from the end
Then starts again with someone new
You see the echo as it continues
Like poetry, it rhymes
https://www.esquire.com/entertainment/a3556/klosterman1107/
Mini-Composition
The poems theme is to keep in you’re comfort zone and not risking the what could happen if you leave. The poem seems to be against thinking outside of the box as it’s not worth the struggles that come with it. The poem is by Adrienne Rich and the poem is a free verse quite abstract and confrontational. In Ghost of a chance, the poet uses an extended simile to demonstrate the discomfort of a man who allows himself to think outside of the box, but mainly a man who allows himself outside of his comfort zone. In the poem, the speaker is watching a man thinking thoughts which may go against what society thinks is “right”. The man then slips into his “old consolations” which are compared to a “fish half dead from flopping”using simile. The man then feels pain, in the form of agonizing air before hes free’d into the sea. Both air and sea are personified in this poem, air is freedom but he feels pain because he’s not in the setting to be thinking these thoughts. They are against what society is “supposed to do”. The man get’s scared of the fact that he’s thinking these thoughts when he shouldn’t. These thoughts are then released into the sea which is described as triumphant. The triumphant sea represents society and the thoughts being kept closed by the society. It is stopping him from having independent thoughts. The man’s thoughts are like fish, they belongs in the sea. The figurative language within the poem displays that a man cannot have ideals greater than society, he like everyone else will just go back to their old ways. This connects largely to Oryx and Crake through explaining the power of humanities, human relations and corporate power. It demonstrates how strong the opinion of others are and how it stops someone from achieving more than they are supposed to. It creates a base level of society that can’t be passed because of how we continue to go back to our old ways. Ghost of a chance by Adrienne rich is a free verse poem that speaks of leaving the comfort zone and how it’s risky due to it being considered as not “right” to society, it uses many figurative devices such as similes and symbolism to compare things and create symbolism and this all leads to it connecting to Oryx and Crake as they both demonstrate the power of humanity, the power of human relations and corporate power.
Love of Jurassic Park
I was interested in the content because of my love for movies and tv shows. The article talks of Jurassic Park, a movie that completely changed the game with the use of CGI and the signature Spielberg filming that’s shown throughout his many movies. The author praises Spielberg and the franchise, telling us he must be part of the vast cult that loves the movies. The author expresses praise by going into detail about what he loved about the movies by showing us that he cares about the attention to detail shown throughout the movies, being very descriptive throughout. He also expresses his love of the camera work used with the dinosaurs by expert cinematographers in the movies, specifically Spielberg, who directed the first movie, which most of us can agree is the best of the franchise. It’s insightful how he talks about the movies and tells us what he likes about it giving us an insight into his motivation to create this article, which is his love of the franchise. The connections I made while reading the article is sharing my love of movies, including Spielberg’s work and the Jurassic Park franchise with the author, the author conditions toward the enormous cult following who even after years continues to be big fans of the movie. He does this by giving us nostalgia reminding us why we love the movies by explaining why he loves the movies.
Interior paradox of modern popculture
https://www.esquire.com/entertainment/a3556/klosterman1107/
I’m interested by how the author feels he has a obligation to read harry potter or watch the movies because they are such an important part of pop culture in our modern world. As the current generation grows up most of them pick up the book or watch the movies having heard of them, also feeling this obligation to be “in the know”. In the case of the author he refuses to watch the movies or read the books even though he knows he should to catch up to the modern pop culture, he has what he calls an “interior paradox” where he contradicts the obligation by simply deciding he doesn’t want to, even though he thinks it would benefit him. The author’s style of writing is very descriptive and insightful by giving his personal opinion on how pop culture (specifically Harry Potter) affects the world and the next generation as it’s so vastly known and praised. The article portrays a very biased opinion on his refusal to be “in the know” about Harry Potter by not engaging in either reading or watching the content of the series, yet it feels completely justified by the fact that he explains how pop culture shouldn’t be an obligation. The article explains how you shouldn’t have to watch specific movies or shows just because they’re depicted by the media as being some of the best of all time, even though in our case if we heard something was one of the best movies of all time we’d most likely watch it. This relates heavily to most of my generations lives as we feel the need to be “in the know” about all that is happening around us, mostly because the media suggests us to do so.
Core Competencies: Tranformations Unit
The transformations unit has impacted my critical thinking as I had to analyze graphs and equations to figure out the transformations that took place. This also helped my creative thinking by pushing me to use transformation equation language/transformation word language to aid in my work. The transformation equation language/transformation word language made the unit much easier as all the questions we’re easier once they we’re all laid out. The language helped my creative thinking as with it I was able to create strategies that made the overall question into one simple equation with the information of all the transformations that took place. Overall the unit helped push me to create strategies and analyze properly while making sure I was precise and checking my work.
Pre-Calc 11 Week #17
This week in PreCalc we started our trigonometry unit, while practicing what we know from previous years we slowly added in new things such as the sine law, this is something completely new that we haven’t done in previous years. The sine law is the following, a/sin A = b/sin B =c/sin C with the lowercase letters being the measurements of each sides and the uppercase letters that happen to be multiplied by sign being the angle for each letter respectively.
If there is a missing angle and not a missing side which is what the sine law is mainly for, you flip it to sin A/a = sin B/b = Sin C/c and it can work to find the missing angle as well. When using the sine law there is 3 equations to start with but once inputting values you only use 2 equations, leaving 1 variable in the full equation.
The sine law is used for triangles with a missing angle or side that aren’t right triangles and have an angle more than 90 degrees
Here is an example of how to use the sine law to find a missing angle
Pre-Calc 11 Week #16
This week in PreCalc 11 we learned how to solve rational equations where fractions with binomial or trinomial numerators or denominators are multiplied or divided by eachother or on other sides of the equal sign. There are two main ways to solve these rational equations, 1 is by cross multiplying which is done when its 2 fractions on opposite sides of the equal sign and the other is to multiply for common denominators which is usually done when there are multiple fractions on one or both sides of the equal sign.
When dividing you flip the fraction that is dividing into and change the division sign to a multiplication sign.
Example,
Pre-Calc 11 Week #15
This week in PreCalc 11 we learned about adding and subtracting rational expressions that have binomial and trinomial denominators. So the first step in any adding or subtracting of expressions, you need to simplify the whole equation by finding common factors in the numerator or denominators.
Example,
Next we need to find a common denominator so we can add just like a normal fraction
Then you just have to simplify it further by taking the brackets out and adding/substracting respectively