Sources:
“Drug Abuse Facts.” – Teen Challenge Canada. N.p., n.d. Web. 8 June 2016.
“Inhalants.” NIDA for Teens. N.p., n.d. Web. 9 June 2016.
“What Are Inhalants?” National Institute on Drug Abuse (NIDA). N.p., n.d. Web. 9 June 2016.
Background music credit: Cold – Jorge Mendez
<<Previous week Next week>>
Here are some strategies you can use to see if an expression is factorable:
In both terms, there is a coefficient of 7, so it becomes the coefficient of the new expression.
2. Difference of squares. If the expression is a binomial that has subtraction between the two terms, then you know that the factored version has both a negative and positive sign:
3. Check for patterns. If the expression is a trinomial with a pattern of 
This week, I learnt a useful trick I could apply anywhere, from this question. Factoring the formula helped put it in a simpler form I could better understand, and organized it into compact parts. This will save time when punching in numbers on a calculator. It will also make sure I don’t mess up a step, since with the old formula, I simply calculated everything in a messy way:
I would normally multiply or take care of exponents, and save the answers in my calculator. Then I would add the two saved numbers together for an accurate answer. However, it can get confusing and I sometimes lose track of what I had already multiplied together. This formula looks much nicer:
Patterns can make math so much more easier, and interesting. They provide shortcuts that solves problems in half the time, and give you pointers to keep you in the right direction.
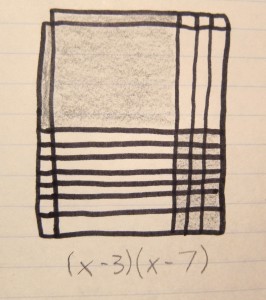
These three algebra tile models show a useful pattern that can be used to figure out which sign to use (negative or positive) when factoring polynomials. If it is completely shaded in, that means the whole expression is positive.
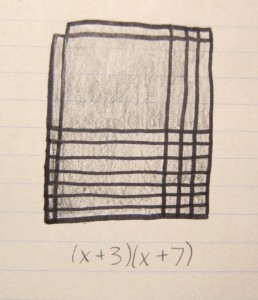
If all the x tiles are shaded in on one side (it can be either horizontally or vertically), then that indicates there is a mix of positive and negative signs.
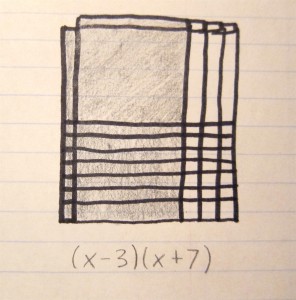
If the model is checkered, with specifically the x squared tiles and ones tiles shaded in, then that means there are only negative signs.
Another pattern which makes expanding polynomials easier is the one similar to FOIL. But instead of individually distributing the multiplication step-by-step, you can simply use basic math to expand.
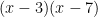
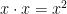
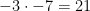
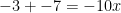
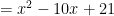
You just multiply the first two terms together, and then the last two together. Then you add the last two terms in each bracket together.
This pattern always works on these simple expressions, and saves a lot of time, especially when solving word problems with many different steps in it. It can take a bit longer to write out the new expression after multiplying, and then circling or labelling to combine like terms. Patterns are useful!
This week I learnt how to use an area model to expand an expression. It’s very useful since it organizes everything so you don’t miss a step while multiplying terms. Heres an example:
Draw a lowercase T and divide the bottom and right according to the number of terms in the expression. Since a binomial is being multiplied by a trinomial, the top is divided in two and the sides are divided in three.
Now plug the numbers into their corresponding spots:
Then, you simply multiply the numbers together! You can almost think of it like playing battleship:
I have colour coded all the like terms together. The ones that are the same colour are added together, and the final answer is 
This week, I got half of the question correct, since my final answer was 
I had been adding and multiplying the exponents together, but that was only half the battle:
But the exponent meant that the binomial is multiplying by itself, so using distribution to solve the problem is the correct way to do it:
