Patterns can make math so much more easier, and interesting. They provide shortcuts that solves problems in half the time, and give you pointers to keep you in the right direction.
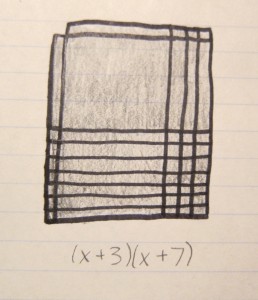
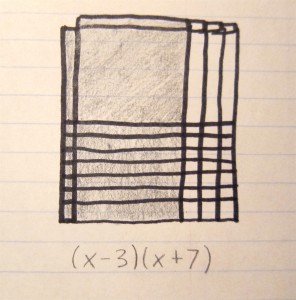
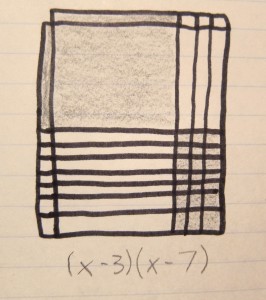
These three algebra tile models show a useful pattern that can be used to figure out which sign to use (negative or positive) when factoring polynomials. If it is completely shaded in, that means the whole expression is positive.
If all the x tiles are shaded in on one side (it can be either horizontally or vertically), then that indicates there is a mix of positive and negative signs.
If the model is checkered, with specifically the x squared tiles and ones tiles shaded in, then that means there are only negative signs.
Another pattern which makes expanding polynomials easier is the one similar to FOIL. But instead of individually distributing the multiplication step-by-step, you can simply use basic math to expand.
You just multiply the first two terms together, and then the last two together. Then you add the last two terms in each bracket together.
This pattern always works on these simple expressions, and saves a lot of time, especially when solving word problems with many different steps in it. It can take a bit longer to write out the new expression after multiplying, and then circling or labelling to combine like terms. Patterns are useful!