This week in pre-calc 11, we learned all about the sine and cosine law

Sine law: 

We use sine law to find either a missing angle or a missing side.

To understand the formula, we must understand that a triangle has 3 sides and 3 angles. The side of an angle is it’s opposite. With this triangle, we can see that the side labeled c is opposite to the angle C.

To find a missing angle, we use the formula: 

To find a missing side, we use the formula: 

We use the sine law when we are trying to figure out an unknown angle or side and the given triangle shows you (or lets you figure out) the information of an angle AND its opposite side.

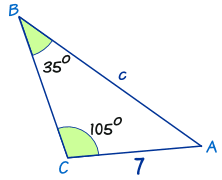
For an example, .

First step would be to determine which formula to use. Since we are missing a side, we will be using .

Next, we would plug in the numbers that we know into the formula:

Since we only really need one equal sign in our equation we can eliminate one part of the formula that we don’t need since it doesn’t give us any useful information. In this example, we could eliminate 

The next step is find c with some basic algebra and some calculations.

To isolate c, we would multiply both sides by

Using a calculators, we can find that

in this week of precalc 11 I learned how to add rational expressions

you want to find your non-permissible values before starting the question

the first step is to factor if possible

the second step is to cross out things if they’re the same but only in that one fraction

now you want to find a common denominator and multiply the fraction to get to the common denominator making one fraction

now you just add the numerators in the one fraction and your finished

this week in precalc 11 I learned about nonpermissible values.

nonpermissible values are numbers that x cant equal because if it does there are no possible solutions.

now the way you find them is by looking at the denominator which could be nx, (x+n)(x-n)

so for the first one x cant equal 0 because the denominator cant equal 0 and 0 multiplied by a number =0. for the second one you have to make sure the denominator doesn’t = 0 so x cant = -n and for the last one its the same thing except x cant equal +n or else it will equal 0.

also there can be more than 1 non permissible values in a equation like  *

so the non permissible values would be 0 and+4

this week in math Precalc I learned about radicals and how to graph them
for example y=

so first you want to graph the parent function 2x+5

now you want to look for your invariant points (-1 and +1) then you want to draw two L shapes not touching the x-intercept or the x=x int asymptotes making this

the red line doesn’t actually touch the x int even if it looks like it does because a radical is just flipping the numbers 2 is now 1/2.

in this week we learned how to graph absolute values

for the first example a linear line y=|x+3|

so first you just graph the parent function y=x+3

when it touches the x-intercept it has to go back up because it always has to stay positive

the right side stays the same because it’s positive and the left side just flips making a v shape

we also learned the absolute value of parabolas, for example, y=|x^2 -3|

so you want to draw the parent function again and just flip the negative parts so they are positive making a w shape

This week we learned how to solve quadratic inequalities.
to do this we graph a regular quadratic just as we learned before
then to find out what side is true its if the Y is greater than, shade in the center if its Y is less than, then shade the outside.

In this week we learned how to graph an inequality.
Say we have 2x + 3y > 6

First, we must make the Y a 0
2x > 6
Then we must divide both sides by 2
x > 3
Then change the > to a =
x = 3
we then repeat the same steps for the Y axis to end up with
y = 2

Once you have these two points plot both on the grid and connect them. after this follow the line to reach each side of your graph.

Next, we must figure out which side is true. to do this we must replace the 2x + 3y with a 0 so we end up with
0 > 6
Now we ask our self, is 0 greater than 6?
since its no, the shaded side will be the side without 0 on it.

In this week we learned how to graph trinomials quicker

for example in this equation
y = 2X^2 + 6X + 8
first of in this equation you can see the Y-axis (8)

Once you find the Y axis you can then convert it to…

y = 2(X + 3)^2 -1

This one shows the vertex (-3,-1) and tells you where the formula will shape and point (2) it shows by looking at the “a” (2).

In this week we learned how to factor Trinomials

For example 16X^2 + 36X + 8

First, multiply 16 * 8 and find the factors of numbers that multiply towards it until you find the factors that add together to create 36.

So 16 * 8 = 128
128 = 4 * 32
4 + 32 = 36

so once you have done this you will end up with 4X and 32X in your empty squares.

and finally, you will end with (4 + 32X) and (4X + 8).