This week in pre-calc 11, we learned all about the sine and cosine law

Sine law: 

We use sine law to find either a missing angle or a missing side.

To understand the formula, we must understand that a triangle has 3 sides and 3 angles. The side of an angle is it’s opposite. With this triangle, we can see that the side labeled c is opposite to the angle C.

To find a missing angle, we use the formula: 

To find a missing side, we use the formula: 

We use the sine law when we are trying to figure out an unknown angle or side and the given triangle shows you (or lets you figure out) the information of an angle AND its opposite side.

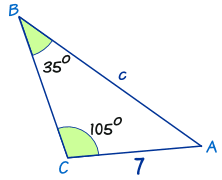
For an example, .

First step would be to determine which formula to use. Since we are missing a side, we will be using .

Next, we would plug in the numbers that we know into the formula:

Since we only really need one equal sign in our equation we can eliminate one part of the formula that we don’t need since it doesn’t give us any useful information. In this example, we could eliminate 

The next step is find c with some basic algebra and some calculations.

To isolate c, we would multiply both sides by

Using a calculators, we can find that

in this week of precalc 11 I learned how to add rational expressions

you want to find your non-permissible values before starting the question

the first step is to factor if possible

the second step is to cross out things if they’re the same but only in that one fraction

now you want to find a common denominator and multiply the fraction to get to the common denominator making one fraction

now you just add the numerators in the one fraction and your finished

this week in precalc 11 I learned about nonpermissible values.

nonpermissible values are numbers that x cant equal because if it does there are no possible solutions.

now the way you find them is by looking at the denominator which could be nx, (x+n)(x-n)

so for the first one x cant equal 0 because the denominator cant equal 0 and 0 multiplied by a number =0. for the second one you have to make sure the denominator doesn’t = 0 so x cant = -n and for the last one its the same thing except x cant equal +n or else it will equal 0.

also there can be more than 1 non permissible values in a equation like  *

so the non permissible values would be 0 and+4

this week in math Precalc I learned about radicals and how to graph them
for example y=

so first you want to graph the parent function 2x+5

now you want to look for your invariant points (-1 and +1) then you want to draw two L shapes not touching the x-intercept or the x=x int asymptotes making this

the red line doesn’t actually touch the x int even if it looks like it does because a radical is just flipping the numbers 2 is now 1/2.