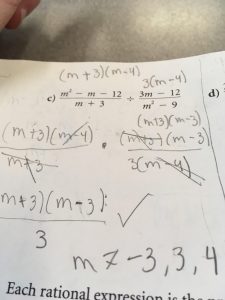Math 11

The Cosine Law week 17

dashao2015 Leave a comment

This week I learned the cosine law and how to solve triangles while using the law. The cosine law is used to solve the third side length of a triangle. There are 2 formulas for the cosine law one is used to solve a side length and the other formula is used to solve a missing angle or \ theta. The formula used for the side length is a2 = b2 + c2 – 2bc cos A.  The beauty of the cosine formula is that you can re arrange and find any letter you want without making any negative variables so it makes it easier. The angle formula is the formula that I used for my example to figure out an angle. And with cosine its not only solving right angle triangles but other ones as well. And if the triangle has 2 angles given to you then you can subtract the 2 angles from 180 to get the third angle so you don’t need to use the cosine law at all. In my example I had to find 2 angles using the rearranged cosine law formula and I substituted the letters to make it less confusing for me. I found solving triangles with the cosine law pretty easy because you just need to substitute the letters that you are looking for.

My example with the rearranged cosine formula. And after you get the answer make sure to inverse cosine to get the angle!

 

Dividing rational expressions week 16

dashao2015 Leave a comment

A couple of weeks ago I learned how to divide rational expressions. The first step is to cross out any numbers that reduce so you can make the fraction smaller, or if its factorable then factor it. The second step is to reciprocal which also means flip the fraction and then after that multiply straight across and if the factored denominator has the same factor at the top then you can cross them out and then after multiply straight across the top and straight across the bottom.

The example I used required me to factor so you can get a better understanding of what I meant.

 

Blog post week 15 solving addition and subtraction rational equations

dashao2015 Leave a comment

This week I learned how to add and subtract rational expressions and how to solve for a variable value. The first step is to make the denominators the same and to do that you multiply it by the lowest common multiple, and then you multiply the top with the same denominators. In my example I show how I did that and then after that I made an equation and since it was a linear equation I had to move the variables to one side and then collect the like terms and after solve for my variable. So it was simple algebra, the only thing I found confusing was multiplying the denominators with the numerators because they had to be the same. Then slowly I understood how to do it and now have a good understanding of which denominator goes with each numerator.

Blog post week 14

dashao2015 Leave a comment

This week I learned how to multiply and divide rational expressions by factoring to get the restrictions for only the denominator.

My example is how to divide rational expressions. The first step is to factor, the second step is to state the restrictions, the third step is to flip over the fraction (reciprocal) and multiply from across to bottom. Then scratch out what is common and whatever is left that is your answer. I find this really easy because I love working with fractions and it is not that complicated. I find multiplication easier than dividing because then you can factor the expressions and then state your restrictions and the last step to multiply and scratch out the common expressions. There is no reciprocal required. And in my example there is a difference of squares so the factored form will be conjugates which is really easy. With this unit factoring is the key component because it tells the most important part the restrictions for x or any variable.

My division example that I used and simplified.

Blog post week 13

dashao2015 Leave a comment

This week I learned how to graph and solve reciprocal functions. So to solve the function you must factor it to get the roots, or also known as the x ints. So the graph has 2 solutions. And to know if a reciprocal function has no solutions that means that it doesn’t factor and has extraneous roots. And if you don’t have an equation but a graph instead you would know that it doesn’t have any solutions if the graph doesn’t cross the x ints. My example I solved had 2 solutions because it had 2 roots.

My example that I used and explained

 

Blog post week 12

dashao2015 Leave a comment

This week, I have learned how to graph the absolute value of a linear function. And since you can’t have negatives the graph goes down and then comes up which makes it a shape of a v. My example that I used was y=3x+3. And then I graphed it and labeled the x int and the y int. Also the domain and range. And its a linear function because it does not have an x^2 so it won’t be a parabola. The domain is always going to be that XER and the range can be that y \ge 0. Or any number greater than zero in this case my range is that y is greater or equal to zero. I can’t wait to learn more of these functions and so far graphing them is easy. And its a lot easier to find the x ints when it is in vertex form because then you can easily plot the vertex on the graph and then convert it to general form to get the y int.

 

 

Blog Post Week 11

dashao2015 Leave a comment

This week I learned how to translate word problems to equations. I found it pretty hard because some of the wording was confusing or I put it in the wrong order. I should do more problems to get the hang of it and to understand it more, and make it easier for me.

Step 1: Underline the key words ex: sum,product,minus, greater or equal to, less then and other important signs.

Step 2: Choose variables ex: x and y or other variables of your choice

Step 3: Then create your equation

After I created the equation I was able to figure out the y int and then graph it.

Here is my example and I underlined the key words that helped me to create the equation.

 

 

 

Blog Post Week 10 – Finding the Discriminant

dashao2015 Leave a comment

Today I decided to do my blog post about how to find the discriminant in a quadratic equation. The discriminant is used to find if an equation has 2 solutions or no solutions. An equation can have no solution if the discriminant is negative and if the discriminant is positive it has 2 real solutions. And if the equation is not equal to zero then you have to rearrange it so it will equal to zero. I did my example with that kind of quadratic equation. Then when you rearrange it you substitute the variables with the numbers given and then you calculate your discriminant and see how many solutions. It was the easiest for me to do because it didn’t involve a lot of steps or any factoring.

My example that I chose to complete and show the steps how to do it.

 

Blog post week 9 Modeling Problems with Quadratic Functions

dashao2015 Leave a comment

This week I learned how to model problems using quadratic functions. The first step you do is make an equation in factor form because it will be a lot easier to find the roots. With the factor form formula you are able to find the axis of symmetry which will be you x intercept.

(x-x1)(x-x2) This formula is the factor form formula. So after you find the value of x you just substitute it into your equation. With my example I first had to use the rise/run to find my slope and after I found my slope I used the slope point formula.

y-y1=m(x-x1) This is the slope point formula.

Then you just substitute your values to get your equation. After you use a formula that helps you find the revenue of a certain object that is for sale. After you got that equation substitute your values again and then find the axis of symmetry or rearrange the equation. Then to find the axis of symmetry take your x value and divide it by 2. Then you will get your price and answer. For my example it has 2 answers but I mostly got $5. In this chapter I found the rearranging confusing but after I did more questions I understand how to arrange from different forms to the forms that I need in order to solve the quadratic equation. And if you get stuck just use standard form to get a vertex and then draw it on your parabola because you will find the axis of symmetry a lot faster and your x intercepts. This is what I learned in Math 11 pre calculus in this week.

 

this week. My example is number 6 in the workbook.

 

Finding parabola characteristics week 8 Block A

dashao2015 Leave a comment

Last week I learned how to find a vertex, the x intercepts, y intercetps, the domain and range, the axis of symmetry, minimum or the maximum and if the parabola opens up or down. By using the formula y=a(x-p)2         

With this formula I am able to find the vertex with the p+q values. The “a” tells me if the parabola compresses or stretches and the (x-p)2 tells me the horizontal translation. The formula at the top is in standard form which is the easiest to use. 

And with the standard form formula you can also use algebra to solve a missing variable so that your equation will be inm that form. In the example below I will show you how to find all of the characteristics of the following equations.

Here is my example and the equation is positive so my parabola will be opening up and if my equation was negative then it will be opening down. The a also tells me if the parabola opens up or down so the formula is easy to understand and use to find all of the characteristics. I also used desmos to see the y int which was 13. Desmos has been very helpful to me because then I can see how the parabola looks like and know the x and y intercepts. The standard form also tells me all of the information and their is enough to graph a lot of points. Remember when you are graphing a parabola make sure to have a lot of points because its a curve and not a straight line and if you are stuck make a table of values and it will make it easier to graph. That is what I learned in class last week and can’t wait to learn more about parabolas.