Month: April 2018
Blog Post Week 11
This week I learned how to translate word problems to equations. I found it pretty hard because some of the wording was confusing or I put it in the wrong order. I should do more problems to get the hang of it and to understand it more, and make it easier for me.
Step 1: Underline the key words ex: sum,product,minus, greater or equal to, less then and other important signs.
Step 2: Choose variables ex: x and y or other variables of your choice
Step 3: Then create your equation
After I created the equation I was able to figure out the y int and then graph it.
Here is my example and I underlined the key words that helped me to create the equation.
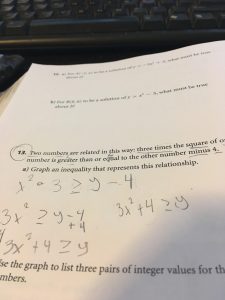
Blog Post Week 10 – Finding the Discriminant
Today I decided to do my blog post about how to find the discriminant in a quadratic equation. The discriminant is used to find if an equation has 2 solutions or no solutions. An equation can have no solution if the discriminant is negative and if the discriminant is positive it has 2 real solutions. And if the equation is not equal to zero then you have to rearrange it so it will equal to zero. I did my example with that kind of quadratic equation. Then when you rearrange it you substitute the variables with the numbers given and then you calculate your discriminant and see how many solutions. It was the easiest for me to do because it didn’t involve a lot of steps or any factoring.

My example that I chose to complete and show the steps how to do it.
Blog post week 9 Modeling Problems with Quadratic Functions
This week I learned how to model problems using quadratic functions. The first step you do is make an equation in factor form because it will be a lot easier to find the roots. With the factor form formula you are able to find the axis of symmetry which will be you x intercept.
(x-x1)(x-x2) This formula is the factor form formula. So after you find the value of x you just substitute it into your equation. With my example I first had to use the rise/run to find my slope and after I found my slope I used the slope point formula.
y-y1=m(x-x1) This is the slope point formula.
Then you just substitute your values to get your equation. After you use a formula that helps you find the revenue of a certain object that is for sale. After you got that equation substitute your values again and then find the axis of symmetry or rearrange the equation. Then to find the axis of symmetry take your x value and divide it by 2. Then you will get your price and answer. For my example it has 2 answers but I mostly got $5. In this chapter I found the rearranging confusing but after I did more questions I understand how to arrange from different forms to the forms that I need in order to solve the quadratic equation. And if you get stuck just use standard form to get a vertex and then draw it on your parabola because you will find the axis of symmetry a lot faster and your x intercepts. This is what I learned in Math 11 pre calculus in this week.
this week. My example is number 6 in the workbook.
STI Project Blk C
 Loading...
Loading...
Finding parabola characteristics week 8 Block A
Last week I learned how to find a vertex, the x intercepts, y intercetps, the domain and range, the axis of symmetry, minimum or the maximum and if the parabola opens up or down. By using the formula y=a(x-p)2
With this formula I am able to find the vertex with the p+q values. The “a” tells me if the parabola compresses or stretches and the (x-p)2 tells me the horizontal translation. The formula at the top is in standard form which is the easiest to use.
And with the standard form formula you can also use algebra to solve a missing variable so that your equation will be inm that form. In the example below I will show you how to find all of the characteristics of the following equations.
Here is my example and the equation is positive so my parabola will be opening up and if my equation was negative then it will be opening down. The a also tells me if the parabola opens up or down so the formula is easy to understand and use to find all of the characteristics. I also used desmos to see the y int which was 13. Desmos has been very helpful to me because then I can see how the parabola looks like and know the x and y intercepts. The standard form also tells me all of the information and their is enough to graph a lot of points. Remember when you are graphing a parabola make sure to have a lot of points because its a curve and not a straight line and if you are stuck make a table of values and it will make it easier to graph. That is what I learned in class last week and can’t wait to learn more about parabolas.
