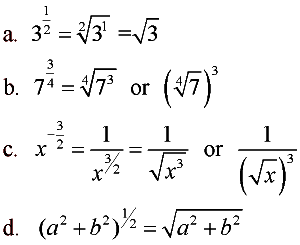
From Fractional exponents to radicals and vice versa.
Today we learned that as exponents can be considered negative, it can also be considered into a fraction. Where the denominator is always the index and the numerator is always the power to the radicand or radical.
In a. you can see that the radical has an index of 2, since in the fraction form the denominator is also two. In class the easiest way to remember this formula is ‘flower power’
This system works for everything, as long as it’s in the brackets, everything inside will be rooted. Unless then only the base of the exponent will be rooted.
How Each Question was delivered:
a: 3 to the power of 1/2 follows ‘flower power’ as the denominator follows as the INDEX and the numerator follows as the EXPONENT, creating a radical
b: 7 to the power of 3/4 follows the same thing, but it only shows that the exponent can be on the 7 or outside the bracket
c: x to the power of the -3/2, the first step for me would to change it into something positive, so you would flip it upside down then following step A or B to complete the question
d: a squared and b squared can be resolved by transforming the terms inside the brackets under the same radical by using the same methods in a or b . Another popular way is to multiply it by everything inside. a squared multiplies 1/2 and repeats for b. which would equal them out since 2 x 1/2=1 so the answer in the end is the same no matter which route you take.
Leave a Reply