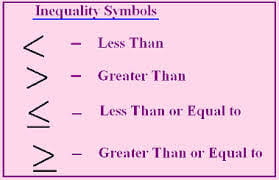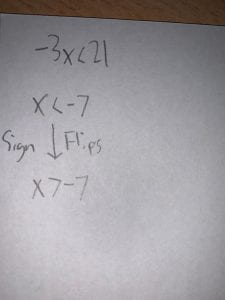Category: Uncategorized
Rube Goldberg Project
First, the ball will roll down A, then bounce on the edge of B because of the momentum and bounce perfectly on to the power switch of B turning off the computer because the ball is attached to a elastic string.
The purpose of this device is meant to turn off a computer.
In this video, the ball is being pulled up from a book because of the elastic string it is attached to, gaining potential energy, then falling onto the power switch of the computer with the pull of the gravity and the mechanical energy, turning off the computer.
What I learned in Grade 9 Linear Relations
What is a Linear Relation
A linear relation is a pattern that increases or decreases by the same amount every time.
What is a T-Chart and How to fill it
When finding the rule for a linear relation, you can put the numbers in a t-chart. A t-chart helps you record your data in one table. This chart helps you find the relationship between x and y. On the left side of the chart is x, and the right is y.

How to find the Rule for a Pattern
The first step is to know how much the pattern changes each time. Once you know how much your pattern goes up/down by you put the number next to x. Next you insert 1 instead of x as it is the first number in the pattern. Example: 6(1)=y. You know that 6(1) does not equal 3. The next step is to find how you get from 6to 3. To get from 6 to 3 you subtract 3. Now add -3 to your rule. Your rule now looks like 6x-3=y. To see if this is correct, try it on the next number.
How to Plot a Point
On a graph, the horizontal line is the x axis and the vertical line is the y axis. The first number on your coordinates is the x number and the second number is the y. Example: 2,3 the 2 is x and 3 is y. The first number tells you which way you are going to go on the x axis. If the number is positive you go to the right and if the number is negative you go to the left. The second number tells you which way you are going on the y axis. If the number is positive you are going up the y axis and if the number is negative you are going down the y axis. If are coordinate is 2,3 you will go right 2 times, and then up 3 times. Once you have done this, you place your point where the coordinates lead.
How to Graph a Linear Relation
To graph a linear relation, put your equation into a t-chart. Once you have a couple pairs of numbers you can insert the points onto the graph. Example, the rule 6x-3=y, the first three numbers are 3,9,15. Now your t-chart has 1,2,3 in the x column, and 3,9,15 in the y column. When you put the two together you get your coordinates. For example, 1,3 2,69 3,15. Once you have these coordinates you can plot them on the graph.
How to Graph Vertical and Horizontal Lines
A vertical line goes across the x axis. This means that the formula you are going to use x = a number. For example x=3. A horizontal line goes across the y axis. This means that the formula you are going to use is y = a number. For example y=-3. This will create a horizontal line to the right and left of -23 on the y axis.
Vocabulary:
X Axis – The horizontal line on a graph.
Y Axis – The vertical line on a graph.
T-Chart – A chart that has two columns.
Quadrant – A graph that is split in 4 parts.
Origin- The middle of the graph.
Plotting – Where you place your point on a graph.
Linear Pattern – A pattern that increases or decreases by the same amount each time.
Increasing Pattern – A pattern that increases each time.
Decreasing Pattern – A pattern that decreases each time.
Horizontal Line – A line that runs from left to right.
Vertical Line – A line that runs top to bottom.
Something Else I learned
Something else that I learned in this unit is restricting your line to between two points. This is useful because without the formula, you will have a long line running from one side of the graph to the other.
Importance of Fasteners
Wood Screws: Screws used for wood and other soft materials.
Machine Screws: Used for the assembly of metal parts.
Self Cutting Machine Screws: Machine Screws with a thread cutting, self tapping point.
Sheet Metal Screws: Designed to be directly driven into sheetmetal. Can also be used on plastic, fiber glass, or wood.
Self Driving Sheet Metal Screws: Just Sheet Metal Screws with a self drilling point.
Hex Bolt: Used with a nut or a tap pole.
Carriage Bolts: Has a spur section which pulls in the material to prevent spinning during installation. Used to fasten wood parts.
Lag Bolts: A heavy duty screw that are used to connect heavy lumber or other heavy materials.
Socket Screws: Are Machine Screws with an internal hex socket.
Set Screws: Used to hold a nub colour, pulley or gear.
Eye Bolt: Used for attaching a rope or a chain.
Eye Lag: Uses wood thread instead of machine thread.
J Bolts: Used for tie downs.
U Bolts: Attaching pipes and other round surfaces.
Shoulder Bolts: To create a pivot point.
Elevator Bolts: Used in conveyer systems.
Sex Bolts: Used for through bolting applications, where a head is desired on both sides of the joint.
Mating Screws: Has a shoulder that matches the diameter of the sex bolt.
What I have learned About Grade 9 Inequalities
What is an Inequality
An inequality compares two values, showing if one is less than, greater than, or simply not equal to another value. Example: 2 > 1.
What the symbols mean
An inequality has 1 out of 4 different signs. The first sign is >, which is the greater than sign. This sign is used when the number on the left is bigger than the on the right. The second sign is <, which is the less than sign. A less than sign is used when the number on the left is smaller than the number on the right. The third sign is ≥, which is the greater than or equal to sign. This sign is used when the number on the left can be greater or equal to the number on the right. The fourth sign is ≤, which is the less than or equal to sign. This sign is placed when the number on the left is less than or equal to the number on the right. Examples: 3 > 2, 7 < 8, x ≥ 13, 9 ≤ x.
How to solve
Solving inequalities is almost exactly like solving an equation; legal moves. The only difference is when you are dividing by a negative, you need to flip the sign. Example, if you have -3x < 21, after you divide and get x < -7 you need to flip the sign, so your answer becomes x > -7
How to graph an inequality
To graph an inequality on a number line, you need to know how to identify what the sign is. If the sign is < or > than you will put an open dot on your graph and if the sign is ≤, or ≥, you will place a closed dot on your graph. Once you know what kind of dot you need, you need to find the number that is the inequality with x. For example x > 10. You would find 10 on your number line. Once you have found 4 draw the dot on top of the 4. The direction your arrow goes depends on the sign. For our example, x > 4 the arrow would go to the right of 4. This is saying that x can be any number to the right of 4.
How to check an inequality
Since solving inequalities are very similar to solving equations, checking is also mainly the same. To check your solution, you replace the variable with your answer. Example: 2x+4 > 8. When you do all your legal moves you end up with x > 2. From here, your answer should be 2. Now you replace the variable with 2 and solve. 2(2) + 4 > 8 turns into 4 + 4 > 8, then 8 > 8.Now you know that your number is right. There is also a second to check and inequality. The second way to check is to make sure the sign is going the right way. To do this you need to put any number that is greater than 2 into the question. Example: 2(10) + 4 > 8 turns into 24 > 8 which is a correct statement.
A Mountain Journey – Questions & Vocabulary
Questions:
1. What was Dave Conroy doing out in the wilderness? (motivation)
Dave Conroy was capturing animals for their fur in the wilderness.
2. At what point does the reader know the protagonist is in serious trouble and not likely to make it to MacMoran’s cabin? (plot)
The point where you know Conroy is in trouble is when you know he can’t make it to the cabin.
3 . What three critical mistakes did Conroy make? What are some of the things he could have done to prevent himself from freezing? (plot)
One mistake that Conroy made was having too much confidence of his ability to make it to the cabin after not stopping when he fell in the river and not realizing that he had hypothermia. If he hadn’t he could have rested and not keep walking to the cabin. Also, if he had stopped after he had fallen into the river, he still would be fine. Him not realizing that he had hypothermia was his biggest mistake because that is how he died. If he had realized this sooner, he could have made a fire before his hands became numb.
4. Determine the elements of plot in this story: exposition, complicating incident, 3 crises, climax, and the denouement.
Exposition: Conroy is outside in the wilderness and the only thing stopping him and what was in his way.
3 Crisises:
1. Conroy fell into a small river.
2. Conroy got to the cabin and saw that it was all gone.
3. Conroy tried to make a fire, but he couldn’t because his hands were too cold.
Climax: He gets to his cabin once its all gone so he decides to hike to another cabin to spend the night. While he was on the way he got tired and lied down to take a rest then he fell asleep.
5. Describe the setting – how does the setting affect the plot and the theme of the story? What is the theme – write a theme statement for this story.
The setting is in Hoodoo creek, Alberta, in the winter. The setting affects the plot by being the antagonist in the story. It also effects the theme by making Conroy try to be tough out the wilderness.
6. Find one example of symbolic setting (concrete place that represents something abstract) and explain its meaning.
The tree that was calling Conroy’s name was a symbolic setting because that is not a normal occurrence and it was a message to stop going.
7. Quote four images from the story that make effective comparisons (figurative language: simile, metaphor, and personification)
Simile: “At every step too, he had broken tail and his skis had sunk a foot in the new snow, white and soft as flour. ”
Simile: “That tree, like a strong and lonely woman, called to his weary body to stop.”
Personification: “The wind was rising with the sundown. It whipped snow against his face, cut through the weave of his 2 woolen mitts, set the forest moaning beside him.”
Metaphor: “The cold was an old man’s fingers feeling craftily through his clothes.”
Vocabulary:
1. eternal p.92: lasting or existing forever; without end or beginning
2. immobility p.93: the state of not moving; motionlessness
3. opaque p.93: not able to be seen through; not transparent
4. reverberation p.93: prolongation of a sound; resonance
5. momentum p.93: the quantity of motion of a moving body
6. cadaverous p.94: resembling a corpse in being very pale, thin, or bony.
7. congregated p.95: gather into a crowd or mass.
8. inundation p.95: an overwhelming abundance of people or things.
9. beggared p.95: reduce (someone) to poverty.
10. filched. P.96: pilfer or steal (something, especially a thing of small value) in a casual way.
Rube Goldberg Reflection
- Things that went well
The machine worked, but because of the last minute adjustments, but because of our mistakes and misplacements, the machine did not work 2/3 of the time.
- Problems that occurred during the process
The lever was not even and centered to the large ramp 2/3 of the time, 1/3 the ball went off course because of this, and the other time the ramp was slightly off centered, but the ball made its way to the multiple small ramps, but, because it was slightly off centered, the ball could not put out then flame.
- Things that you’d do different next time
Glue all of the buildings together.
- Testing results
It worked 1/3 of the time.
Socials Studies 9 Core Competencies Reflection
| Name: Connor O’Charchin | Date: Dec.20 |
|
How does the artifact you selected demonstrate strengths & growth in the communication competency?
In what ways might you further develop your communication competency? |
Self-Reflection
Describe how the artifact you selected shows your strengths & growth in specific core competencies. The prompt questions on the left – or other self-assessment activities you may have done – may guide your reflection process.
I used critical thinking in my board game researches because I looked for information in 2 different chapters in the Horizons textbook to look for information. I took many notes for the research and put lots of time and effort into the researches. I can improve on this by staying focused in class to get more information. |
|
How does the artifact you selected demonstrate strengths & growth in the thinking competencies?
In what ways might you further develop your thinking competencies? |
||
|
How does the artifact you selected demonstrate strengths & growth in the personal & social competencies?
In what ways might you further develop your personal & social competencies? |
Publish Your Self Assessment
You will now attach and/or embed your self-assessment to the bottom of the blog post with the artifact you have chosen. You may choose to make this post private or public. After placing your artifact on a blog post, follow the instructions below.
- Categories – Self-Assessment
- Tags – Now tag your post using the tag that corresponds to the competency that you have written about. You can choose more than one. Please use lower case letters and be exact.
- #creativethinkingcc
- #communicationcc
- #criticalthinkingcc
- #socialresponsibilitycc
- #personalidentitycc
- #personalawarenesscc
- Use the Add Document button located at the top of your post page and embed your self-assessment at the bottom of your blog post.
- Publish
Socials Studies 9 Core Competencies Reflection
| Name: Connor O’Charchin | Date: Jan 17 |
|
How does the artifact you selected demonstrate strengths & growth in the communication competency?
In what ways might you further develop your communication competency? |
Self-Reflection
Describe how the artifact you selected shows your strengths & growth in specific core competencies. The prompt questions on the left – or other self-assessment activities you may have done – may guide your reflection process.
In socials 9, I have used communication by talking with my peers and asking them for help if I am stuck. When I am stuck, I try to solve the problem on my own, but if I get stuck, I ask my peers to give some help, so I can understand and help others if they need my help. I can improve this by focusing more in class so I understand the concept. |
|
How does the artifact you selected demonstrate strengths & growth in the thinking competencies?
In what ways might you further develop your thinking competencies? |
|
|
How does the artifact you selected demonstrate strengths & growth in the personal & social competencies?
In what ways might you further develop your personal & social competencies? |
Publish Your Self Assessment
You will now attach and/or embed your self-assessment to the bottom of the blog post with the artifact you have chosen. You may choose to make this post private or public. After placing your artifact on a blog post, follow the instructions below.
- Categories – Self-Assessment
- Tags – Now tag your post using the tag that corresponds to the competency that you have written about. You can choose more than one. Please use lower case letters and be exact.
- #creativethinkingcc
- #communicationcc
- #criticalthinkingcc
- #socialresponsibilitycc
- #personalidentitycc
- #personalawarenesscc
- Use the Add Document button located at the top of your post page and embed your self-assessment at the bottom of your blog post.
- Publish
What I learned about grade 9 polynomials
Vocabulary:
Degree: The largest exponent attached to a variable in an expression.
Constant: A term without a variable.
Coefficient: The whole or large number in a term.
Leading coefficient: The coefficient at the start of the expression (most left).
Binomial: When the number of terms in an expression is 3.
Trinomial: When the number of terms in an expression is 2.
Monomial: Is equivalent to one term.
How to use algebra tiles:
You will have 3 types of algebra tiles. 1, x and x². Expressions will usually have the largest amount to least amount. So the order will be in x², x then 1/whole numbers. With x² tiles, since they are the largest, they will also be physically the largest pieces. You will follow the expressions instructions. If it tells you to place 4 x’s, then place 4 x’s. But when an negative number is involved, all you need to do is flip the tiles backwards.
Add polynomials:
When starting out learning polynomials, it is good to sort the alike terms with each other. Example: 2x² + 3x + 3x². The first thing you should do is sorting the terms with the other ones that are alike. This step is not mandatory, but will help you when starting out learning to simplify polynomials. After sorted by amount, the expression should turn into 2x² + 3x² + 3x. After sorted, add the coefficients that have the same variable and exponent to each other. It should look like 5x² + 3x. Starting with small expressions is easier to learn than trying to simplify larger ones.
Subtracting polynomials:
Just like simplifying every other polynomial expression, it’s good to sort the terms. Example: 7x + 5 + 4x² – (2x² – 2 + 3x). In subtracting, all of the terms inside the bracket that is after the subtracting symbol gets flipped to its opposite number. 7x + 5 + 4x² + (-2x² + 2 – 3x). After doing this, just add and follow what the expression is. 4x² + (-2x²). 7x + (-3x). 5 – 2. The simplified version of the expression should be 2x² + 4x + 3.
Multiplying polynomials:
2(4x + 2). Multiplying polynomial expressions is almost like multiplying normally. The only difference is the variable.
Using algebra tiles for learning large multiplying expressions is very helpful. When you use algebra tiles, model the expression in a shape in a rectangle. In the example, you would take 2 small tiles and place them on the left side. On the other side, you would take 2 long tiles and 2 smaller ones and make a line with them. To simplify the expression, you must fill the space with more tiles. But, using algebra tiles and multiplying polynomials is mainly used for large expressions.
Without algebra tiles, you need to multiply normally. When there are variables, it is different. When the number that is multiplying has no variable attached, you follow whatever the variable is. In the example above, the simplified version is 8x + 4.
Some expressions might have you multiply by 2 numbers. Example: 3x + 2(4x + 2)
First, you multiply the number on the far left of the expression by the numbers inside the brackets. After that, you do the same the the number on the right; multiply them by the numbers inside the brackets. Once you have both of these numbers, you add them. The simplified version would be 12x² + 14x + 4.
Dividing polynomials:
4x + 2
_______
2
Using algebra tiles for dividing is almost pointless. Dividing polynomials is very simple if you can divide whole numbers. You would divide these numbers normally except for the variables. Just like multiplying, the same rules apply except of adding the variables, you subtract. So in the expression above, the simplified version is 2x + 1.