This week in Math 10, I have chosen to talk about systems of linear equations.

Like previously covered in other blog posts, a linear equation is an equation with variables that can be graphed as a straight line on a plane. A linear equation system can be described simply as two lines. A solution to a system is the point where both lines intersect. Whether or not it has a solution can be determined with the following criteria.

1. If both lines have the same slope (m) but not the same y-intercept (b) then there is no solution.
2. If the slopes of the lines are different, then there is exactly one solution.
3. If both lines are identical, there is an infinite number of solutions since they are, in essence, the same line.

Here is an example of the system comprised of and

The solution here is the point (1.875, -1.313) in this case, as it is where the lines intersect. Here is another one, with instead of

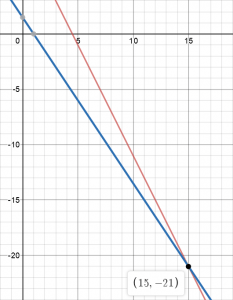With this one, it is instead (15, -21) as the solution.