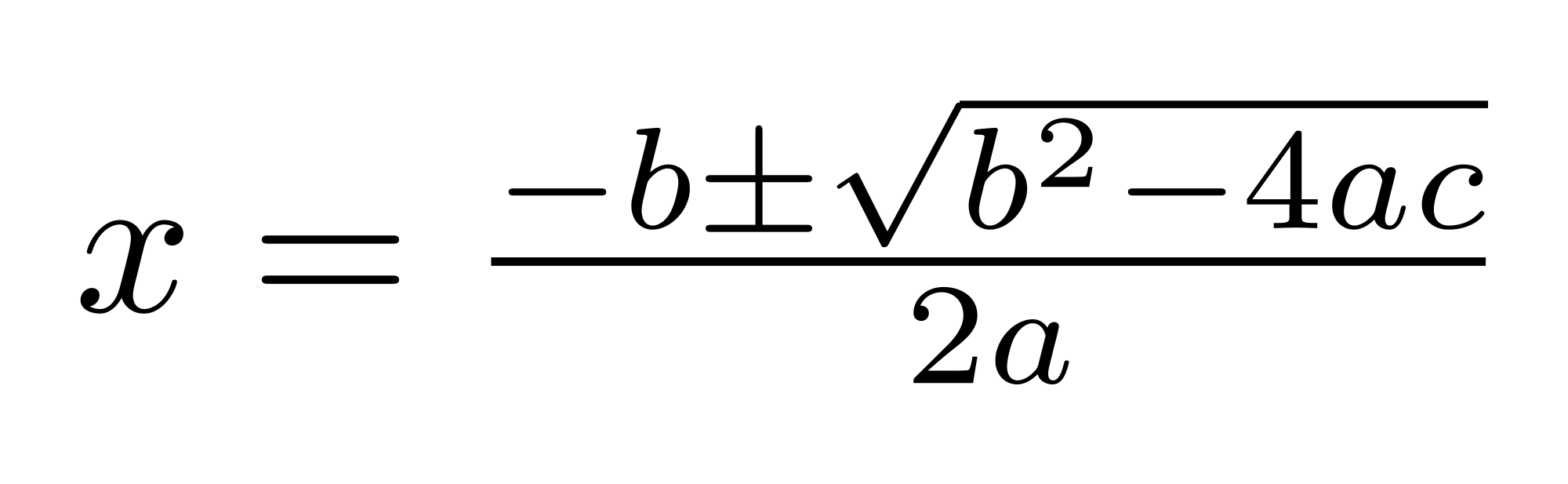October 30

Newton’s Laws

Newton’s first law :

objects at rest tend to stay at rest. So this tennis ball here is not moving it was at rest and is staying at rest unless another source applies force.

Newton’s first law wouldn’t always apply to this if another force applies itself to make it accelerate or if it’s moving down a friction less surface.

In the video there are no unbalanced forces so nothing will change in the law.

Newton’s second law.

f=ma. force is equal to mass times acceleration. In this example we rolled a ball across the floor and we found that the lighter the mass the easier it was to accelerate the object. As you can see in the video we barely pushed the ball and it had quite a bit of speed. Newton’s second law wouldn’t always apply if the mass is constantly changing like a snowball rolling down a snowy hill is gaining mass.

Newton’s third law, every action has an equal and opposite reaction. As you can see in the video when the ball falls to the ground the ground reacts and pushes the ball back up now if those were the only variables then the ball would have bounced back up to where it originally was but since there is gravity that pushes the ball back down the reaction is significantly reduced. Newton’s third law wouldn’t apply when there is no gravity.

I found that the first and second laws are very similar because in both of them they would either stay at rest or in motion unless acted upon.

 

Category: Grade 11 | LEAVE A COMMENT
October 27

Precalc 11 – Week 8

This week in precalc 11 we learned about the standard form aka Vertex form.

The standard form is the most useful form for finding graphs.

the formula is  y = a(x-p)^2 + q.

everything in the formula says something about the graph. Starting with a, a will usually tell you how thin or how wide a graph is. If there is no number there a = 1. And when a = 1 then we can see the width by following this: 1, 3, 5. those numbers show how far over you will go every time. so you go up 1 over 1 up 3 over 1 up 5 over 1 and you should hit the graph each time. but if a = 2 then you would go 2, 6, 10. Notice how when a is > than 1 the graph become longer and skinnier. when a becomes smaller it becomes wider.

the next important piece is p. P is sometimes difficult to understand. It determines if your graph slides to the left or right and is also the line of symmetry. so if you have (x-3)^2 and so 3 is your p variable then you would move 3 to the right. I know you see the negative and think you will be going left but you go just what p is if it was $latex (x – -3)^2 then you would move 3 to the left because p was -3.

now we have come to q. q determines where you are on the axis and this one doesn’t become weird like p with the negative in front you just put it wherever it says it is so if it’s -5 then you have the graph at -5.

Category: Grade 11, Math 11 | LEAVE A COMMENT
October 20

Week 7 in precalc 11

This week in precalc 11 we had review for our unit test and then we relearned graphs after that. We also learned about the parabola. A parabola is a U shaped curve on a graph that is symmetrical on either side. when we look at that graph we should be able to find the vertex, line of symmetry, x-intercept, y-intercept, domain and range. I found that when we first worked on the graphing that it was decently easy but when we progress it becomes more difficult (as always).  One thing to note is that the vertex is one of the most important pieces of information and it can be the highest point on the graph or the lowest (min, max).

Category: Grade 11, Math 11 | LEAVE A COMMENT
October 17

Week 6 in precalc 11

This week in math 11 I learned about the quadratic formula.

the quadratic formula looks like this :

Image result for quadratic formula

in order to fill in the variables you need to know what is what.

so when you’re looking at an equation it will look like

ax^2 + bx + c = 0.

your a variable is obviously the number in front of the x^2 but if there is no number in front of it, a = 1. b is the second variable and it is the one in the middle of the equation and c is separate on its own.

It takes more time then completing the square and factoring but it is a good way to get the correct answer since you fill in all the variables and get a more direct answer.

Category: Grade 11, Math 11 | LEAVE A COMMENT
October 15

Week 5 in Precalc 11

This week in math 11 I learned the acronym CDPEU we can easily remember the acronym by using the expression “Can divers pee easily underwater”. The acronym means Common factors, Difference of squares, patterns, easy and ugly. this is meant for when we have an equation like x^2 + ax + b.

C – common factors. If you see any common factors reduce them, it will make the question a  lot easier.

D – Difference of squares, a difference of squares is a bit different. It’s when we have two squares in the equation that subtract for example : x^2 – 81 would be (x + 9) (x – 9)

P – Patterns, patterns are pretty self explanitory but, what it is saying is to look for a pattern to more easily figure out an equation such as a trinomial equation. x^2 + x + b.

E – Easy, easy questions are question that will easily factor to add to the middle term or subtract and multiply into the last term.

U – Ugly, an ugly question is more difficult and can take more time. You may need to do different strategies because these questions can go into fractions.

Category: Grade 11, Math 11 | LEAVE A COMMENT
October 4

Week 4 in Precalc 11

This week in math 11 we learned about adding and subtracting radicals and we also learned how to multiply and divide.

this week we were not solving equations we were simplifying them. so when we had the equation 3 \sqrt {2} + 2 \sqrt {2} – 5 \sqrt {2} then we would simplify that to \sqrt {2}

the way I solved it was by using like terms.

adding and subtracting radicals is quite simple. It’s just combining like terms. so if we have 5 \sqrt {3} – 2 \sqrt {3}, we would get 3 \sqrt {3}.

 

 

Category: Grade 11, Math 11 | LEAVE A COMMENT