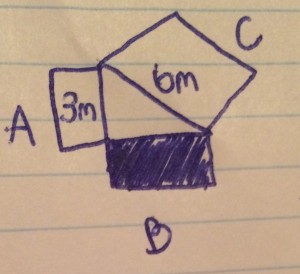
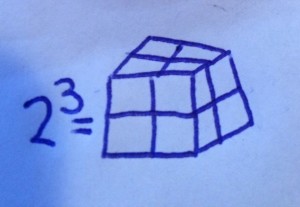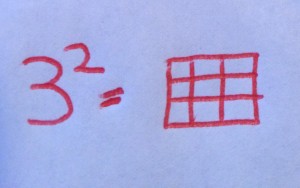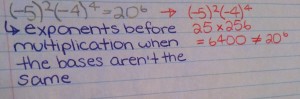Article #1:
Personally I think this affects me because I should keep an eye out about who is “friends” with me or my friends and if I come across and account of someone that I don’t trust or that seems suspicious I should reach out to the adults in my life and get help because this year I have learned a lot about Digital Footprint and how whatever we put online we can never get back, so I think that it is important to not react to people that are fake online but instead to get help. I think it is also important to take from this that you can’t believe everything you read online and to get multiple sources from different people and websites instead of trusting social media. Because nowadays anyone can go online and say whatever they want even if they are not educated on the topic so it is important to not believe what you read from the first source that you see. Also its important not to talk to strangers online because you don’t know who is behind the computer.
Article #2:
I think this article was a lot like the first one and being aware about what we see online. I think it is important not to retweet or re share things that you are not fully aware about, because you never know what the person is thinking or who they are or if their story is real. Its important not to trust the tabs as they say and not to believe everything you hear on the news right away because information gets turned and changed very quickly. Also you wouldn’t know the whole story right after the event its important to wait a day until all the information is right and out. In the article they said that you wouldn’t know all the facts right off the bat so the information you are getting is probably fake or just for attention.”Common sense says that a version that’s published a few hours after an incident isn’t likely to have been done properly.” I agree with the part that said that we need to slow that and wait to get our facts correct rather then quick because people start to speculate and create rumours that spread throughout the world now that we can all write things within 30 seconds and have them on the internet for anyone to see.
Overall I think the message that I received from these articles is that it is important to get your information from the right sources and not from social media platforms just hours after the events that occur. Its important to get information from people who are credible and people who you know are who they say you are.