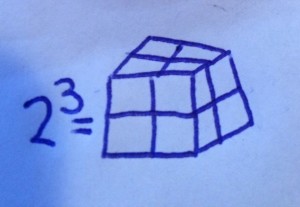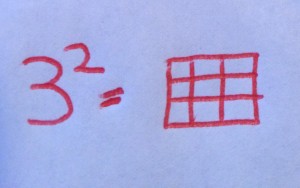Protected: Math Journal #5

November 15, 2016

Static electricity – PocoOpolis 500

November 12, 2016

Down below is the written out experiment:

Static Electricity:

Purpose: The point of this experiment is which materials when rubbed together ten times will create enough static charge to attach small pieces of paper to it.

We have conducted three parts of this experiment; one with wool, one with silk and one with fur. We will commence with the wool.

The independent variable is what the stick is made up of, the dependant variable is small pieces of paper and the controlled variables are wool and the amount of times we rub the two materials together.

Our hypothesis was that when we rub the materials against each other, glass will have the most friction with wool.

The first step in this experiment was to find all our materials. We used wool, and then ebonite, copper, aluminum, plastic, wood, glass, Lucite and acetate, as well as the small pieces of paper. We then one by one tested each rod/material with wool by rubbing the two objects together. We then put the rod a couple cm above the pieces of paper to see if the static charge picked them up. We tested that with each rod/material, but only lucite was slightly affected, with a small flinch in the materials. On a scale of 1-10 it was about a 0.5.

Results: From this experiment, we found that wool was very unreactive and did not hold a lot of static charge.

The most important finding is that only Lucite did anything and it was barely a flinch. Another important finding was that that none of the others were reactive. We also when rubbing it with copper, we didn’t manage to rub it the full 10 times so that might have had an affect on it.

Materials	Amount of charge
Wool + Ebonite	0
Wool + Copper	0
Wool + Aluminum	0
Wool + Plastic	0
Wool + Wood	0
Wool + Glass	0
Wool + Lucite	0.5
Wool + Acetate	0

For our conclusion, wool and Lucite when rubbed together create the most static charge. We found that wool didn’t create a lot of a static charge.

Our hypothesis was incorrect, as glass and wool when rubbed together did not create any static charge.

Further question:

If a carpet creates static electricity when we walk on it with our socks, how come it didn’t react with any other materials.

Silk:

The independent variable is what the stick is made up of, the dependant variable is small pieces of paper and the controlled variables are the silk and the amount of times we rub the two materials together.

Our hypothesis was that Silk and Aluminum when rubbed together would create the most static charge.

The first step in this experiment was to find all our materials. We used silk, and then ebonite, copper, aluminum, plastic, wood, glass, Lucite and acetate, as well as the small pieces of paper. We then one by one tested each rod/material with silk by rubbing the two objects together. We then put the rod a couple cm above the pieces of paper to see if the static charge picked them up. We tested that with each rod/material, but none of the materials created any static charge. The paper had no reactions with any of the rods.

Results: Silk is very non reactive and did not create any static charge when rubbed together with another material.

The important findings are that nothing created a static charge.

Materials	Amount of charge
Silk + Ebonite	0
Silk + Copper	0
Silk + Aluminum	0
Silk + Plastic	0
Silk + Wood	0
Silk + Glass	0
Silk + Lucite	0
Silk + Acetate	0

For our conclusion, none of the materials rubbed together with silk were reactive. Our hypothesis was incorrect, as Silk and Aluminum when rubbed together had no static charge, and was not the most reactive. I want to know why there was no charge whatsoever, was it something we did or something to do with silk?

Fur

Our hypothesis is that when fur and Lucite are rubbed together it will create the most static charge.

The independent variable is what the stick is made up of, the dependant variable is small pieces of paper and the controlled variables are the fur and the amount of times we rub the two materials together.

The first step in this experiment was to find all our materials. We used fur, and then ebonite, copper, aluminum, plastic, wood, glass, Lucite and acetate, as well as the small pieces of paper. We then one by one tested each rod/material with wool by rubbing the two objects together. Next, we put the rod a couple cm above the pieces of paper to see if the static charge picked them up. We tested that with each rod/material, but only lucite and fur was affected. It had a much bigger reaction that previous times, and picked a fair amount of small pieces of paper. On a scale of 1-10 it was about an 8.

Results: When fur and Lucite are rubbed together they create a static charge.

Important findings: Only Lucite and Fur created static charge, and no other materials when rubbed with fur were reactive.

Materials	Amount of charge
Fur + Ebonite	0
Fur + Copper	0
Fur + Aluminum	0
Fur + Plastic	0
Fur + Wood	0
Fur + Glass	0
Fur + Lucite	8
Fur + Acetate	0

In conclusion Fur + Lucite were the most reactive out of everything we tried, this was why we used it in our race. I am curious to know why fur reacted so well with Lucite but not with anything else.

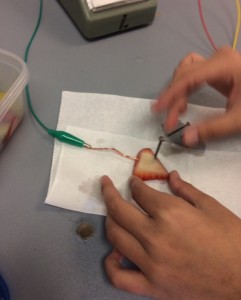
Currents from the Kitchen

November 10, 2016

Hypothesis: When we test out the fruits; grapes, kiwi, strawberry and apple the most acidic fruit will produce the most voltage because acids make ions/charged particles, these charged particles are the same as the ones that are produced in an electric current therefore I believe that the Kiwi will produce the most volage because a kiwi is sour therefore it is acidic and makes ions. There is also a chance that the strawberries can produce the most voltage because they are acidic as well.

Experiment

Results

Strawberries: -1 (v)

Kiwi: +o.5 (v)

Apple: +0.25 (v)

Grape: + 0.25 (v)

Most Important Findings: Strawberries were the only negative number on the dial and made the most movement. Kiwi had the highest positive movement with +0.5. The negative and positives have to do with the alligator clips. If you switch them they will be opposite.

Questions

Our group did the experiment with 4 different types of fruits, kiwi, strawberry, apple and grapes. I brought in the kiwis and the strawberries. None of these fruits were able to make the bulb light up, this is because fruits don’t produce enough voltage to light up a bulb. We were able to tell how much energy it was producing through the amount of movement the arrow on the voltage meter was producing. One way to improve this experiment so that the results could be more accurate would be to use the same size of piece of fruit for each type because maybe if we had a bigger sized kiwi it would have been able to light up the bulb, but the apple was way bigger than the grape and maybe that’s why the apple did better. We could also be more accurate with the angle we put the nail into the fruit.

Electricity is produced by a chain of electrons moving from point a to b to create a current. In this experiment electricity was produced from the acid in the fruits. The type of reaction that occurs in fruits so that they are able to create electricity is oxidation-reduction. There are two types of cells that can facilitate this type of reaction, galvanic cells and electrolyte cells. Galvanic cells are spontaneous cells that act as the battery and are able to create a charge by themselves. Electrolyte cells require electricity in order for them to have a charge. This is experiment used a closed circuit because it consisted of a series of wires connecting to one another and the fruit allowing electricity to flow through.

We can use this information in our everyday lives to help us realize that electricity can come from the most commonly used things in our life.

Extra observations:

Grapes and Apples were the exact same
We had to play around with the way we clipped the wire onto the nail so that it could power the dial
We didn’t have time to try the lemon ourselves but it seemed that the lemon worked the best.
We were able to do this experiment by creating a circuit
If we had put two nails into the fruit it wouldn’t have worked because they are the same materials and would repel.

Everything I know about exponents

November 9, 2016

1. Represent repeated multiplication with exponents

You can take repeated multiplication and turn it into an exponent by counting the number of times you multiply a number by itself which becomes the base and use the number of times as the exponent.

Ex: $5 \cdot 5\cdot 5\cdot 5$ would be $5^4$ because there are 4 5’s.

2. Describe how powers represent repeated multiplication

Powers represent repeated multiplication in the exact opposite way the number of the exponent is the amount of times you multiply the base number by itself.

Ex: $3^6$ would be $3\cdot 3\cdot 3\cdot 3\cdot 3\cdot 3$ because 6 is the exponent so there are 6 3’s.

3. Demonstrate the difference between the exponent and the base by building models of a given power, such as $2^3$ and $3^2$

The base is equal to the amount of side lengths of the model and the exponent is the amount of sides the model has.

Therefore $2^3$ as a model is:

and $3^2$ as a model is:

4. Demonstrate the difference between two given powers in which the exponent and the base are interchanged by using repeated multiplication, such as $2^3$ and $3^2$ .

The difference in the powers $2^3$ and $3^2$ is in the first power $2^3$ , 2 is the base and 3 is the exponent, therefore 2 is the number you are multiplying by itself 3 times because 3 is the exponent so it would be $2\cdot 2\cdot 2$ which is equal to $8$ Whereas in the second power $3^2$ , 3 is the base and 2 is the exponent, therefore it would be $3\cdot 3$ which is equal to $9$

5. Evaluate powers with integral bases (excluding base 0) and whole number exponents.

Evaluating powers with integral basses and whole number exponents works by using repeated multiplication.

$\langle {-3} \rangle^2$ → ${-3}\cdot {-3}$ = $9$

$\langle {-2} \rangle^2$ → ${-2}\cdot {-2}$ = $4$

$\langle {-1} \rangle^2$ → ${-1}\cdot {-1}$ = $1$

$1^2$ → $1\cdot 1$ = $1$

$2^2$ → $2\cdot 2$ = $4$

$3^2$ → $3\cdot 3$ = $9$

6. Explain the role of parentheses in powers by evaluating a given set of powers such as $\langle -2\rangle ^4$ , $\langle -2^4 \rangle$ and $-2^4$

When the exponent is $\langle -2\rangle ^4$ it is ${-2} \cdot {-2} \cdot {-2} \cdot {-2}$ which is equal to ${+16}$ , because 4 is an equal number of negatives, this is because the – and the 2 are together in parenthesis and the exponent is outside of both of them. $\langle -2^4 \rangle$ $-2^4$ are the same you do BEDMAS because it is exponent first you go $2^4$ first which is equal to ${+16}$ and then you multiply 16 by it’s coefficient which is -1. Therefore $-1\cdot 16$ is equal to ${-16}$

7. Explain the exponent laws for multiplying and dividing powers with the same base.

The law for multiplying powers with the same base is keeping the base adding the exponents.

$2^6$ • $2^3$
$2^{6+3}$
$2^9$

With a coefficient you would multiply the coefficients by each other.

( $5$ ) $2^6$ • ( $6$ ) $2^3$
$2^{6+3}$ and $5 \cdot 6$
( $30$ ) $2^9$

The law for dividing powers with the same base is subtracting the exponents.

$2^6$ ÷ $2^3$
$2^{6-3}$ or could be demonstrated with repeated multiplication $\frac{2\cdot 2 \cdot 2\cdot 2 \cdot 2\cdot 2} {2 \cdot 2 \cdot 2}$
then you would eliminate the corresponding and be left with $2^3$

With coefficients you would go:

( $30$ ) $2^6$ ÷ ( $5$ ) $2^3$
$2^{6-3}$ or could be demonstrated with repeated multiplication $\frac{2\cdot 2 \cdot 2\cdot 2 \cdot 2\cdot 2} {2 \cdot 2 \cdot 2}$ and then you go $\frac {30}{5}$
then you would eliminate the corresponding and be left with ( $6$ ) $2^3$

8. Explain the exponent laws for raising a product and quotient to an exponent.

When raising a product or quotient to an exponent you use the power law, the rules for the power law are to keep the base multiply the exponents.

Example of power law:

$\langle 3^2 \rangle ^5$ → $3^{2 \cdot 5}$ → $3^{10}$ = $59049$

9. Explain the law for powers with an exponent of zero.

Any power with the exponent of 0 is equal to 1 unless the base is equal to 0.

This is because $\frac {3^2}{3^2}$ when doing BEDMAS becomes $\frac {9}{9}$ which is equal to 1. So when using the quotient law $3^2$ – $3^2$ is equal to $3^0$ which makes it equal to 1.

10. Use patterns to show that a power with an exponent of zero is equal to one.

A pattern of powers with the same base demonstrate that when dividing the answer by the exponent you will get 1 when it comes down to zero as the exponent

$2^8$ = $256$

$2^7$ = $128$

$2^6$ = $64$

$2^5$ = $32$

$2^4$ = $16$

$2^3$ = $8$

$2^2$ = $4$

$2^1$ = $2$

$2^0$ = $1$

Each time you go down you divide by the base number so in the case 2 so when it comes to zero the answer is 1.

11. Explain the law for powers with negative exponents.

Any base except zero raised to a negative exponent equals the reciprocal of the exponent so that it becomes positive.

ex: $2^{-3}$ becomes $\frac {1}{2^3}$ which equals $\frac {1}{8}$

12. Use patterns to explain the negative exponent law

When the exponent in the power is negative you must switch it to it’s reciprocal so that the answer can be positive. If the bases are the same the pattern will be divide every answer by 2 to get the one down.

$2^{-1}$ = $\frac {1}{2^1}$ = $\frac {1}{2}$

$2^{-2}$ = $\frac {1}{2^2}$ = $\frac {1}{4}$

$2^{-3}$ = $\frac {1}{2^3}$ = $\frac {1}{8}$

$2^{-4}$ = $\frac {1}{2^4}$ = $\frac {1}{16}$

$2^{-5}$ = $\frac {1}{2^5}$ = $\frac {1}{32}$

$2^{-6}$ = $\frac {1}{2^6}$ = $\frac {1}{64}$

$2^{-7}$ = $\frac {1}{2^7}$ = $\frac {1}{128}$

$2^{-8}$ = $\frac {1}{2^8}$ = $\frac {1}{256}$

$2^{-9}$ = $\frac {1}{2^9}$ = $\frac {1}{512}$

13. I can apply the exponent laws to powers with both integral and variable bases.

The exponent laws can be applied to both integral and a variable bases because the laws work on the exponent not concerning the base as long as the bases are the same.

Ex: $2^3$ • $2^6$ $2^{3+6}$ = $2^9$

With a variable: $x^3$ • $x^6$ $x^{3+6}$ = $x^9$

14. I can identify the error in a simplification of an expression involving powers.

Error’s made in evaluating powers are either because of the product law, quotient law, power law, zero law, or negative exponents.

Here are examples of me correcting errors in expressions involving powers:

Example of power law:

Example of quotient law:

Example of product law:

Example of zero law:

Negative exponent:

15) Use the order of operations on expressions with powers.

Using order of operations is using BEDMAS. You use BEDMAS on expressions with powers when the bases of multiplication/division expressions aren’t the same or when you are adding and subtracting powers no matter what the base.

Example of different base mistake and correction:

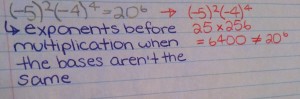
fullsizerender-6

Example of adding powers:

fullsizerender-14

Example of subtracting powers:

fullsizerender-15

16) Determine the sum and difference of two powers.

There is no law for finding them sum of two powers you must simply use BEDMAS so you evaluate the exponents first and then add or subtract them for your answer. Therefore to solve this equation you have to do the exponents first and then add them together.

$3^2$ + $4^2$

$9$ + $16$

$25$

17) Identify the error in applying the order of operations in an incorrect solution.

Order of operations is BEDMAS, Brackets, Exponents, Division &Multiplication {in the other they happen} Addition & Subtraction {in the order they happen.} However if any of the laws apply you must do those first.

18) Use powers to solve problems (measurement problems)

To find the area the blue part of the square you have to go $6^2$ ,because 6cm is the measurement of the side lengths of the full square, minus (4) $2^2$ because there are 4 mini squares in white with equal side lengths of 2cm.

$6^2$ – (4) $2^2$

= $36$ -16

= 20

To find the volume of the cube you have to go $4^3$ because a cube is made up of three equal sides.

$4^3$ = 64

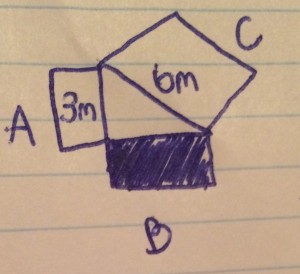
To find the length of a triangle with squares you have to use the pythagorean theory which is $a^2$ + $b^2$ = $c^2$ . But because this figure is missing angle B not angle C you have to use subtraction and go $c^2$ – $a^2$ = $b^2$ .

= $6^2$ – $3^2$

= 36m – 9m

=25m

But 25m is the area of the square however we are looking for the side length so we have to find the square root of 25 which can either be 5 or -5 but because this is a figure it has to be greater than 0 and only 5 is therefore the answer is 5m.

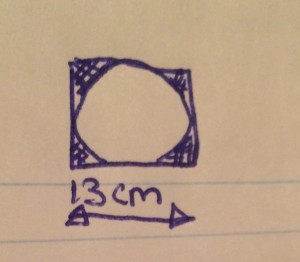
The final measurement I will demonstrate is finding the are of the blue part of the figure down below showing a circle inscribed in a square meaning it’s touching the edges of the square perfectly. The whole measurement of the figures side lengths is 13 therefore it would be $13^2$ minus pi multiplied by the radius of the circle squared which would be ${6.5}^2$ because the radius is equal to half the diameter which was 13.

= $13^2$ – π ( ${6.5}^2$ )

= 169 – π (42.25)

= 169 – 132.73

= 36.27 $cm^2$

19) Use powers to solve problems (growth problems)

My pet hamsters weight triples once a month. It weighs 20 pounds now how much will it way in:

a) 2 months b)4 months c) 6 months

a) 20 x $3^2$

b) 20 x $3^4$

c) 20 x $3^6$

Growth problems can be solved by using exponents because in this example because my hamster started at 20 pounds and is tripling every month so at 2 months it becomes 20 x $3^2$ 20 for the amount of pounds, 3 for the tripling and to the power of 2 because it has been 2 months of tripling which means it has to be 20 x 3 x 3. Therefore with any amount of months it would be 20 x $3^x$

20) Applying the order of operations on expressions with powers involving negative exponents and variable bases.

$\frac {\langle a^{-5} b \rangle ^{-3}}{\langle a^4 b \rangle ^{-2}}$

When you are applying the order of operations on expressions with powers involving negative exponents and variable bases the first thing with this question you do is the power law.

$\frac {\langle a^{15} b^{-3} \rangle }{\langle a^{-8} b^{-2}\rangle}$

Then you would apply the quotient law by subtracting the exponents

$a^{15- -8}$ → $a^{15+8}$ → $a^{23}$

$b^{-3- -2}$ → $b^{-3+2}$ → $b^{-1}$

Then you put the all the positive powers on top and the powers with the negative exponent on the bottom.

$\frac {a^{23}}{b^{-1}}$

Because it is $b^{-1}$ you don’t need to keep the -1 therefore you’re final answer is:

$\frac {a^{23}}{b}$

….Anything else that you know about exponents.

A base raised to 1 is always equal to the base.

Ex: $5^1$ = $5$

Because $5^1$ with repeated multiplication is just $5$

1 raised to any exponent is always 1.

Ex: $1^5$ = $1 \cdot 1 \cdot 1 \cdot 1 \cdot 1$

Because $1 \cdot 1 \cdot 1 \cdot 1 \cdot 1$ = $1$

No matter how many times you times $1$ by $1$ the answer is always $1$ .

A coefficient is a short cut for repeated addition

Ex: $\langle 5 \rangle 3^2$ = $3^2 \cdot 3^2 \cdot 3^2 \cdot 3^2 \cdot 3^2$

LateX coding

November 4, 2016

Example 1: exponents

$5^2$

Example 2: fractions

$5^{20}$

Example 3:

$\frac{3}{5}$

Example 4: $3x^2\cdot5x^7$

Example 5: $3x^2\div5x^7$

Example 6: Bigger size

$6^{-5}$

Example 7:

$6^5$

Example 8:

$6^5$

Réflexion – Monsieur Lazhar

November 4, 2016

Voici mon opinion sur le question: “Quelle est la différence entre éduquer et enseigner? Pensez-vous que le système scolaire devrait seulement enseigner aux élèves et non pas les éduquer”

My SSEP experience

November 4, 2016

1. Define

screen-shot-2016-11-05-at-9-02-16-pm

We need an experiment that can be done in micro gravity that is going to really catch the reader and be beneficial to todays world.

Micro Gravity is where there is asserting of next to no gravity or very weak gravity such as in a orbiting spacecraft, or when something is moving very quickly from up to down in the air, there is micro gravity then too.

The control groups in this area are how much of each substance we are going to use and the amount of time we are going to keep the substances together for observation. The experimental group is the setting because when we do the experiment on earth the setting will be with gravity however on the ISS it will have no gravity.

The way that are experiment well win out is by writing out our proposal with all the benefits that science will get by doing our experiment so we have to find an experiment that is going to benefit science. We also need a why because when there is a why it makes the proposal more powerful.

2. Dream

Starting out my group and I brainstormed so many different ideas: Plants and their growth time, electricity and being able to power places from space, things with liquid nitrogen, gas reaction, cooked food, cooking food, if substances could develop in space, perishable foods, electronics, boiling water, lighting a match, tying your hair, static electricity, can your phone work, tv with antennas, water balloons, bacteria and stem cells, all in micro-gravity settings.

One of the subjects that stood out very boldly for me was substances developing. My group wanted to go towards the substances bacteria or stem cells. In the end we researched two big ideas, if we could develop stem cells in space and if we could infect bacteria with harmless viruses could infect bacteria. With the stem cell research the question we wanted to propose had already been done a couple of months ago so we looked into bacteria, pili, auto-agglutination and how viruses could help to kill of bacteria.

Here is a ton of research done on stem cells ad bacteria.

3. Document

The steps of this project went as follows:

•Introduction to the program: We were introduced by our teacher Mr. Robinson

•Attending the SSEP Workshop: at the workshop we got lectures by SFU students talking about what happens to the human body in space, bacteria in space and the look of earth from above. We also learned about what happens when you light a match in space which was something I had been interested in so it was so cool to see, then we learned about living organisms in space and what happens to them in micro gravity. I took lots of notes for later so that I could take them back to by group.

•Putting the proposal together: We wanted to include viruses in our proposal, so reaching out to SFU student Miguel we were inspired to do the question can a harmless virus infect bacteria in a micro gravity setting. This question was going to take a ton of research in finding out the right information so we got straight to work and with a lot of effort we came to deliver our proposal.
screen-shot-2016-11-05-at-9-32-18-pm

4. Design and Deliver

Like I said before I learned about this opportunity through my science class from my teacher Mr. Robinson. With a few of my classes I attended a SSEP camp on a pro-d day to learn about a few of the experiments that had been tried in space from SFU profs and students. We learned about the kind of projects that they are interested in.

With a few of my classmates we did a research project on dividing root cells in micro-gravity. Which was a SSEP project won by a grade 7 class in flagstaff Arizona in 2014. Their objectif was to see if onion root cells would divide with zero gravity and if the experiment was a success, they wanted to see if there are any mutations during the replication of DNA when on the International Space Station. I reached out to the teacher of the class Susan Brown from Northland preparatory academy, she was very helpful and answered our questions in a few emails back and forth. This was a very amazing experience for me being able to talk to someone about research that they had done someone that lives in a whole other country.

We have chosen to research and propose to the SSEP competition is too see the effects of a harmless viruses infecting Vibrio Choleria which is a Bacteria, in a micro gravity section. This is because we think that it can be a very good medical breakthrough helping preventing many bad bacteria from infecting our bodies. We believe It could start a new topic in scientific and medical research which is very important.

We reached out to Miguel a student at SFU a contact given to us by Mr. Robinson, Miguel helped us with some of our re search explaining many of the components of what the bacteria has to produce so that the virus can infect it. He also generously offered to provide us with the substances we needed.

We then wrote an experiment, I wrote the paragraph on our coverage about the begging of our proposal, the page and a bit about the question we are addressing and some of the experiment design. Writing the proposal took a lot of research and work but it was really beneficial to have everything written out so that we could read through our whole plan which was finally coming together.

We have now shared our experiment with the school bored who edited it and a few more staff at our school, my whole group contributed to adding corrections to this document and it is now fully together which is a really accomplishment for my group and I.

5. Debrief

I have enjoyed this project a lot because it has given me many opportunities, being able to learn how to put together a 10 page proposal, how to research independently with no text books to guide you only the internet and a million different search options as well as how viruses are able to infect bacteria which was super advanced considering this research is currently being done by students at SFU and I am only in grade 9. The process went fairly well we had a good time coming up with ideas for this project and amazing responses from our contact at SFU. In my opinion the dividing of the work could have been more fair however in the end we all had a part in it. Everyone did have something to contribute to our group. What went well was really our drive as a team because we were really into making this project the best we possibly could and are looking forward to seeing results come out of this. I also think it was excellent being able to email Miguel because again learning from an SFU student is pretty cool! This has been something so new to me so I am very proud of our teams successful completion of this proposal. We ended up making it to the top 30 out of 280 proposals. Which is an awesome accomplishment for only grade 9’s.

Here is a PDF version of our proposal if you are interested in reading it.

ssep-final-proposal

screen-shot-2016-11-05-at-9-40-37-pm All of the comics were created by Ashiana Sunderji using storyboardthat.com .

TOKTW 2016

November 3, 2016

Name of your host: Ayaz Sunderji Relationship to you: Father

The Interview:

1. What is your job title?

He is a Wealth Planner at Vancity Credit Union.

2. What is your job description?

Helping members with their financial well being, by creating a plan thats based on their personalized goals and dreams. The process that he uses involves understanding the members personalized needs & expectations and ensure that the investment recommendations are aligned with values that are important to you.

3. What are the duties and/or tasks you perform at your job?

Preparing RISK questionnaires, which explains the members comfort zone and taking risk.
Researching investment options and providing recommendations of investment options.
Timely executions of investment purchases and sales.
Insuring investment compliance.

4. What qualifications do you have for this job in the following areas:

a) training?

On the job training, by fellow colleagues, the investment department and attending workshops taught by the industry.

b) education?

Certified financial planning designation through self studies and the financial planning standards council, a degree in bachelor arts in economics from University of victoria , Canadian investment security through the Canadian securities Institute.

c) experience?

In the financial industry since 1992. Mutual Fund License since 1995. Ismaili volunteer for the BC Economic Planning board.

d) skills and attributes (personal qualities)?

Patience, Knowledgable, Resourceful, People Skills, Listening, Communication, Good understanding about finance and math.

5. What are some of the things you like about the job?

Building relationships
Following the Markets
Vancity as the organization

6. What are some of the things you dislike about this job?

Administrative
Paper work follow-up
Limited investment options

7. How do you anticipate this job changing in the next 5 years or so?

Already seeing changes and the biggest one has been technology, the advent of robo-advisors and lower cost investment options. In the future it will empower people to do investment themselves and the technology is advancing so you can get you’re on advice without seeing someone so to be successful you will need more education and how to utilize the technology to you’re advantage.

What I know and want to know about electricity!

November 2, 2016

Electricity Mind Map

Here is my embedded mind map on what I know and want to know about electricity, I am looking forward to the electricity unit because it is a very practical science that we see in our everyday lives. Click on the photos for a closer up look!

Picture citations:

http://assets.inhabitat.com/wp-content/blogs.dir/1/files/2015/11/Electric-Shock.jpg

http://images.clipartpanda.com/tension-clipart-xcg85aAcA.svg

http://xstdx.deviantart.com

http://www.spiritualityhealth.com/sites/default/files/styles/header_image/public/Sustainability.jpg?itok=6jT7FqEo

http://image.shutterstock.com/z/stock-vector-blue-circuit-board-vector-seamless-pattern-with-glowing-connectors-tileable-technology-background-202788337.jpg

http://cdn2.hubspot.net/hubfs/522699/EDU_Blog_Assets/Summer_Learning_Series/Electricity/187bzswqhpil0jpg.jpg

https://cdn.vectorstock.com/i/composite/88,69/question-mark-vector-1068869.jpg

http://www.aouaga.com/anniversaire/images/balloons_BD.png