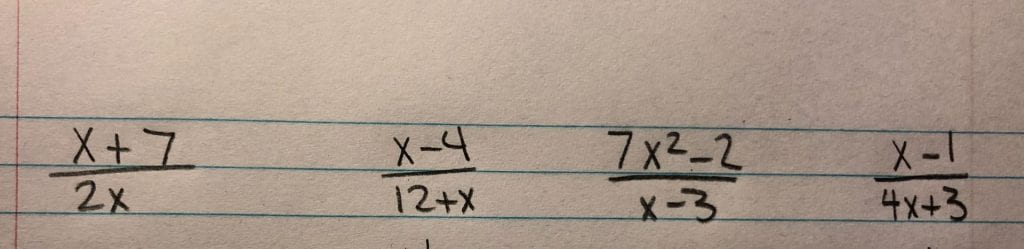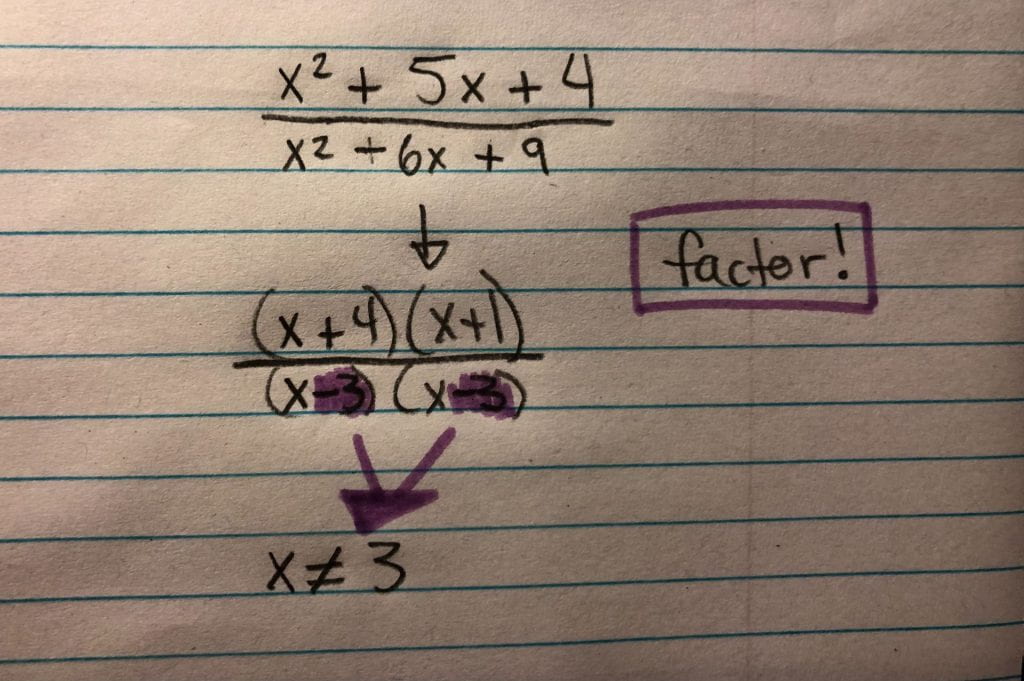In this week of precalc 11, we learned how to solve rational expressions, which are fraction questions with variables. One thing in specific we learned about was non-permissible values. These are values that x cannot be in each equation. First, here are some examples of what rational expressions can look like:

These expressions cannot have square roots, or exponents that are variables.

A non-permissible value is also known as a restriction, the domain, or values that the expression cannot be defined by. This means there are certain numbers, that when put in place of x, make the denominator zero. When the numerator is zero the equation can still be simplified. However, when the bottom of the fraction (the denominator) is zero, this is not possible. Therefore, these are non-permissible. When you write these restrictions, use the equal symbol with a line through it, meaning “x cannot be equal to…”

Here are the non-permissible values for the expressions shown above:

For example, in the second expression, x cannot be -12. If it was, it would look like this:

Since the denominator is now zero, which is impossible, it means -12 is the restriction on this expression. There can also be multiple restrictions, depending on the fraction and number of variables. The last example had a fraction as a restriction, which is not as easy to solve in your head. This is how I solved to find -3/4:

Here are a couple more examples: