Most important things in each chapter:

Chapter I:
Prime numbers – a whole number that has only 2 factors
Composite number – a whole number that has more than 2 factors
Prime factorization – there are 2 ways to do it: division table & tree diagram
Lowest Common Multiple – a number that is a multiple of two or more numbers
Greatest Common Factor – the greatest factor that divides two numbers
Repeating decimals – decimals that have a recurring pattern of digits
Non-repeating decimals – decimals that have no recurring pattern of digits
Terminating decimals – decimals with a finite amount of digits
Non-terminating decimals – decimals with an infinite amount of digits
Real number system – it includes R, 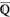, Q, I, W, N
How to simplify roots – 
MOST IMPORTANT THING – flower power, root is always on the bottom

Chapter II:
Multiplication
Division
Power
Negative
Fraction

Chapter III:
How to convert a number to scientific notations – 
How to convert to another unit – 6780cm = 67.8m, 0.91km = 910m, etc.
How to calculate surface area and volume –
Volume of prism: volume = area of base x height
Surface area of prism: add all the surfaces
Volume of cylinder: volume = area of base x height
Surface area of cylinder: area of side + 2 x area of base
Volume of pyramid: x volume of prism
Surface area of pyramid: area of base + area of triangular faces
Volume of cone: x volume of cylinder
Surface area of cone: area of base + area of curved surface

Chapter IV:
Sine ratio – opposite side/hypotenuse
Cosine ratio – adjacent side/hypotenuse
Tangent ratio – opposite side/adjacent side

Chapter V:
Variable – a letter that represents one or more numbers
Algebra expression – 2a-b+4
Numerical coefficient – the number that multiplies the variable
Monomial – polynomial with 1 term
Binomial – polynomial with 2 terms
Trinomial – polynomial with 3 terms
Polynomial – polynomial with 4 or more terms
Degree of a monomial – the sum of exponents of its variable(s)
Degree of a polynomial – the degree of the term with highest degree
Constant term – a term of degree zero(no variable present)
Leading coefficient – coefficient of the term with highest power of variable
Simplifying – 

Chapter VI:
Factoring polynomials – 

Chapter VII:
Relation – the mathematical relationship between 2 quantities
Independent variable – the variable used for inputs in a relation
Dependent variable – the variable used for outputs in a relation
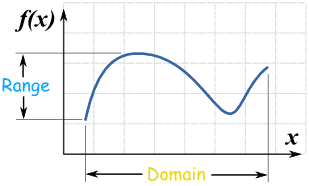
Domain – the set of all possible values for x
Range – the set of all possible values for y

Chapter VIII:
positive slope – goes up from left to right
negative slope – goes down from left to right
zero slope – horizontal line
undefined – vertical line
Slope –

Chapter IX:
y-intercept form – y = mx+b
Slope-point form – m(x-x) = y-y
General form – ax+by+c = 0
Standard form – ax+by = c

Chapter X:
Substitution – a simple way to solve two equations if there is coefficient of 1
Step 1: Choose the simpler equation and express one variable in terms of other
Step 2: Substitute the expression from step 1 into the other equation
Step 3: Solve the single variable equation
Step 4: Substitute the solution from step 3 into the equation in step 1 to find the value of the other variable
Elimination – a way that you can always use, especially without coefficient of 1
Step 1: If necessary, multiply each equation by a constant to obtain coefficients for x or y that are identical
Step 2: Add or subtract the two equations to eliminate one of the variables
Step 3: Solve the resulting equation to determine the value of one of the variables
Step 4: Substitute the solution into either of the original equations to determine the value of the other variable

Things I have learned this week:

-How to find the distance between two points

examples:

(1,6), (1,9)
Subtract the y values then you will get 3 or -3, since this is a distance, there is no negative values so the answer is 3.

(20,2),(5,2)
Subtract the x values and the answer is 15.

(2,5),(3,9)
Find the difference between x values and then find the difference between y values. Then use pythagorean theorem to find the length of the line segment. So the answer is

-How to find slopes

(2,5),(7,20)
You have to find the rise(difference between y values) and run(difference between x values), then do . So the answer is

REMEMBER: YOU HAVE TO DO THE SUBTRACTION IN ORDER

Important things about slopes:

positive slope: goes up from left to right
negative slope: goes down from left to right
zero slope: horizontal line
undefined: vertical line

Things I have learned:

-Factoring polynomial expressions:
I did some simple questions

e.g.

The first one what I did was finding the greatest common factor that the equation has, which is 4. The second one is same as the first one, and the greatest common factor is .

Here is another example I found in the internet:

For this example, 3 is the greatest common factor.

Even though these questions are not new for me, it still helps me. I didn’t do factoring for a while, so these questions allow me to practice more. I have to find the GCF in each question, it is similar to Chapter 1 (Number), it’s pretty much the same thing.

Continue reading Week 8 review →

Things I have learned:

-Find an angle of a triangle

To isolate x, I put to the other side of the equations and changed it to

This is pretty much the same as the last one, I put to the other side of the equation and changed it to

1.

To isolate , the Sin has to move over to the other side of the equation, and it becomes

2.

To isolate , the has to switch with

3.

To isolate , 50 has to move over to the other side of the equation, and it changes from division to multiplication.

Things I have learned:

-Trigonometry:

Sine ratio = opposite side/hypotenuse

e.g. opposite side is 80 % of hypotenuse

Cosine ratio = adjacent side/hypotenuse

e.g. , adjacent side is 60 % of hypotenuse

Tangent ratio = opposite side/adjacent side

e.g. , opposite side is 40% of adjacent side