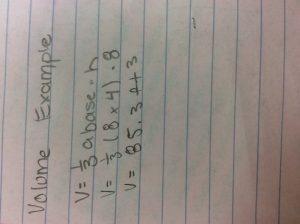4D6E9939-05D2-4072-923C-C4F021731A21-2jb62k0 16243B4C-34F0-45F3-BA4A-ADCFDEDCF93D-1m97swt 41417783-7095-465F-9522-94A81E859712-1hv1j3r F5754EF9-E488-43BB-AF4F-8E2F38A9B689-100t2dt
Category Archives: Uncategorized
Constructive and destructive interference waves
71624CFC-6B05-4567-9B76-70110330DEF1-1t6pdw6
Destructive interference: a crest and trough meet ( the waves are “out of phase “), the energies combine to work against each other – they tend to cancel out
513776FF-CC06-4D1F-AB02-DD87E2120DA4-1a4r4xh
Constructive interference: when a crest from one source meets a crest from another source, the energies combine to displace the medium ( the energies are additive )
AE533E51-4E4B-489B-B13A-0279E2D708CD-1vrzlx5
Standing waves : when interferencing waves have the same amplitude and wave length l, resulting interference pattern remains nearly stationary and is called as standing wave interference pattern ; a node or nodel points is a point that remains at rest throughout the interference of the pulses
Pre-Cal, Week 8
Pre-Cal, Week 7
During Pre-Cal this week i learned how to solve a chart with the properties of quadratic functions. To chart a quadratic equation you have to know how to tell when the table of value is showing a quadratic equation, instead of a linear equation. A linear equation in a table of value always has a y value (the output) that goes up or down by the same amount each time in the first differences. A quadratic equation in a table of value always has a y value that goes up or down by the same amount each time in the second difference. Below is a example of both a linear equation, and a quadratic equation charted.
When solving for quadratic functions, you should remember that the x intercept is always equal to y=0 and the y intercept is equal to x=0 (when solving). To find y you simply plug x into the given quadratic function. Below are some examples to visualize how I would solve for y using the table of values and quadratic function.
Polynomials
In our third lesson of polynomials we learned how to FOIL. Foiling is another method to multiply polynomials using distributive property that’s easy and effective. It makes it easier for you to see exactly what you are multiplying rather than visualizing it in your head.
The method used in the distributive propter can be simplified using the acronym FOIL.
(a + b)(c + d) = ac + ad + bc + bd
F – first term in each bracket
O – outside terms
I – inside terms
L – last term in each bracket
Here are two examples:
(4x + 1)(x – 5)
= 4x^2 – 20x + x – 5
= 4x^2 – 19x -5
(3a + 6b)^2
= (3a + 6b)(3a + 6b)
= 9a^2 + 18ab + 18ab + 36b^2
= 9a^2 + 36ab + 36b^2
Measurement (second half)
In our seventh lesson of measurement we learned how to find the surface area and volume of a rectangular based pyramid. It takes a while and you have to make sure that your formulas are correct to get the right answer. A trick is to write out everything you do. For example you can directly draw the shape of the face it is that you are trying to calculate the area of. This helps to keep track of everything you do and makes it easier to visually see.
Surface Area:
First you have to find the two slant heights of the pyramid. A rectangular based pyramid has two slant heights because the base side lengths are not the same. You find the slant heights by using pythagorean theorem on each triangular face.
Once you find the two slant heights, you find the area of each triangular face. Then you add those to the base area. (Make sure to put the coefficient 2 in front of each triangular face’s area. You do this because it tells you that two of the four triangular faces have the same area.)
You add the each face by writing out how to get the area of each triangular face and then the area of the base. You write them all out side by side and simplify where you can. Lastly you multiply the numbers left after you have simplified.
The number that is left is the surface area of the rectangular prism.
I know this sounds hard, so an example will make it easier to see.
Volume:
To get the volume of a rectangular based pyramid you multiply 1/3 by the area of the base by the height of the pyramid.
You should already have the area of the base from finding the surface area, so we just use that to easily find the volume. (You should be able to do the whole equation on your calculator.)
Here is an example using the same dimensions that I used for finding the surface area above.
Measurement (first half)
In our third measurement lesson we learned how to use a micrometer to measure objects. It can be tricky at times but once you get the hand of it it’s pretty easy.
The object that is being measured is placed between the anvil and spindle.
Then the first thing you do is look at the course reading. The value you take is the last fully visible line on the sleeve.
Next you figure out the barrel scale reading by looking at the reference line on the sleeve. The line that it matches up with on the barrel scale is the number that you take. If the line is in the middle of two numbers, you take the number that the line is closest to.
Lastly you add the course reading and the barrel scale reading to get the micrometer reading.
Here is an example along with a picture to show you where all the parts are on a micrometer.