Grade 11 – Page 2 – Aliessah's Blog

Category: Grade 11 (Page 2 of 3)

Week 10 – PreCalc 11

By aliessahv2016

On April 22, 2019

Factoring has been an important part in PreCalc 11 so far and will probably be in the future as well. Although we have had a lot of practice with them, there are some trinomials that are not as easy to factor as we are used to.

Example:

$(x-6)^2 + 7 (x-6) + 10$

Step 1: Create a Variable in the Expression

The polynomials that we are used to factoring are the ones that have the pattern that follow $ax^2 + bx + c$ . Even though we don’t have that pattern in this equation we can make it so that is does. We can do this by substituting something common. Something that’s common in this expression is the $(x-6)$ . We can make $(x-6)$ equal any variable. In this case let’s make $(x-6) = x$ . So wherever we see $(x-6)$ we switch it for x

$x^2 + 7x + 10$

Now the expression follows the pattern that we are familiar with we can factor as usual.

Step 2: Factor

To factor we have to find a number that when added together equal seven and when multiplied equals 10. In this case the numbers are 5 and 2.

$(x+2)(x+5)$

Step 3: Substitute

We can’t forget about the term that we substituted. Since we made $x = (x-6)$ , everywhere we see x in the factored expression we have to switch it for $(x-6)$

$latex ((x-6) +2)((x-6)+5)

Step 4: Simplify

The only thing left to do is to simplify the expression.

$(x-4)(x-1)$

Week 9 – PreCalc 11

By aliessahv2016

On April 14, 2019

In Math 11, Uncategorized

This week in PreCalc 11, we reviewed and practiced how to read a graph and make an equation in the different forms.

The three forms that we worked with this unit was:

standard form or vertex form- 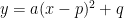$y = a (x-p)^2 + q$ ,where (p, q) is the vertex of the parabola, and a is the stretch value. It’s the easiest equation to graph because we are given a starting point and the pattern that it goes up by.

general form- $y = ax^2 + bx + c$ . A, B, and C are three real numbers. Once these are given, the values for x and y that make the statement true express a set of (x, y) points which form a parabola when graphed. It’s the most useless equation to graph because we are only given the y-intercept and can’t do much else unless it’s converted to one of the other forms.

factored form– $y = a(x-x1)(x-x2)$ . x1 and x2 are the opposite of the x-intercepts of a graph. If the x intercepts are +3 and +5, then x1 would be -3 and x2 would be -5, and the a value is the stretch value. This equation is useful only when given the x-intercepts and is used mostly when trying to search for the a value as long as there is another point given along the parabola to substitute y and x for to find a.

It’s simple to convert the equations between each other because it uses all the skills that we have learned and used earlier in the semester.

Example:

Step 1: Turning It Into Vertex Form

First we have to look at the vertex and see how far it has moved from (0,0). In this picture the vertex has moved 3 units to the left and 2 units down. The 3 units left is our p-value and the 2 units down is our q-value. If we put it into the vertex equation equation, we are left with:

$y = a(x-p)^2 +q$

$y = a (x-(-2)^2 + (-2)$

$y = a (x+2)^2 - 2$

Now we have the a-value left to find. If the a-value is one then the pattern the parabola would go up is up 1 over 1, up 3 over 1, up 5 over 1, up 7 over one, etc…Typically the amount the first jump goes up by is usually the a-value. If the first jump is up 2 and over one, then the pattern is probably 2. That means the original pattern of up 1 over 1, up 3 over 1 would be multiplied by 2 so the 2 pattern is up 2 over one, up 6 over one, up 10 over one, etc… In this case the pattern is 2 because the first jump is over up 2 over one so that’s the a-value. That means the complete vertex equation is:

$y = 2 (x+2)^2 - 2$

Step 2: Convert Vertex Form into General Form

To convert from vertex form to general form is quite simple since it’s mostly expanding and simplifying.

Now that we have $y = 2 (x+2)^2 - 2$ , you just expand and simplify!

$y = 2 (x+2)^2 - 2$

$y = 2 (x+2)(x+2) -2$

$y = 2 (x^2 + 4x +4) -2$

$y = (2x^2+ 8x +6)$

$y = 2x^2 + 8x +6$

Now we have general form of the equation!

Step 3: Turn the Equation into Factored Form

There are 2 ways that we can turn the graph into a factored form equation

First Way:

The first way is to factor the general form:

Step 1 is to factor out the 2 from the equation

$y = 2x^2 + 8x +6$

$y = 2 (x^2 + 4x + 3)$

Step 2 is to find two numbers that when multiplied equal 3 and when added equal 4. In this case, it’s 3 and 1.

$y = 2 (x + 3)(x + 1)$

Step 3 is to find a number that when added to or subtracted from +3 and +1 will equal zero. In this case, the answer is -3 and -1. That means we have found the x-intercepts. We also found out the stretch value.

Second Way:

Second way to get it into factored form is to look at the graph and find the x-intercepts. The x-intercept is where the parabola crosses the x axis. There may 2, or one, or even none. In this case, there are 2 and the x-intercepts are -3 and -1.

Since we are given the x-intercepts we can place them directly into the equation

$y = a (x - x1)(x - x2)$

$y = a (x- (-3)(x - (-1)$

$y = a (x + 3)(x + 1)$

We also know the a-value which is 2 so we can put the a value in. But if we didn’t have the a-value then we could put in another point and substitute x and y for the coordinates, but we know a so we don’t need to do that.

$y = 2 (x + 3)(x + 1)$

Now we have the factored form, and we know how to convert between the rest of equations!

Week 8 – PreCalc 11

By aliessahv2016

On April 6, 2019

In Math 11

This week in PreCalc 11 we learned the properties of quadratic functions and how to analyze the quadratic equation. We learned that when are given the quadratic equation in vertex form then we can graph the equation.

Last unit we learned the quadratic equation $ax^2 + bx + c = 0$ , this unit we learned $y = a(x-p)^2 + q$ . This is combination of the equations $y = (x-p)^2, y = x^2$ , and $y = x^2 + q$ . These equations are all very important in graphing the curve the equations make.

Example 1:

$y = x^2$ (parent function: creates the most basic parabola)

$y = x^2 + 3$ (addition to the parent function)

Explanation 1:

What this equation tells us is based on the +3 at the end of it. This +3 is the vertical translation which means its moving the vertex from (0,0), as it would be in the equation $y = x^2$ because the +3 is replaced with a O, to (0, 3). It moves the y-intercept, in other words, it moves the vertex up or down. If the equation was $y = x^2 - 3$ then it would move the vertex down to (0, -3).

*vertex is either the highest point or lowest point of the parabola

*parabola is the curve the equation makes

*y-intercept is the point where the parabola crosses the y axis

Example 2:

$y = (x - p)^2$ $y = (x-3)^2$

Explanation 2:

The part that tells us about the graph is the -3. This -3 is the horizontal translation which means it moves the vertex from (0,0) to (3,0). It moves the x-intercept, in other words, it moves the vertex left or right. the reason that it is a positive three, but the equation has a negative 3 is because when you place a +3 in the equation $y = (x-(+3)^2$ , the negative overtakes the positive. If it was a -3 then two negatives make a positive so it would be $y = (x+3)^2$

*x-intercept is where the parabola crosses the x axis

Example 3:

$y = ax^2$

$y = 2x^2$ (tall and skinny)

$y = 1/2x^2$ (wide)

Explanation 3:

The 2, in this case, is telling us about the stretch reflection which means that it tells us how wide the parabola will be or how skinny it will be. If the a value is greater than 1 then it’s tall and skinny. If a is less than one and greater than 0 then it’s wider.

That’s why when we are given an equation in vertex form ( $y = a(x-p)^2 +q$ ) then we can easily graph it. It’s called vertex form of the equation because you are given the vertex (the opposite sign of the p value is the x value and the q is the y-value). From the equation we are also given the stretch value which tells us how wide or skinny the parabola is going to be and also tells us the pattern we need to follow to get the correct function. The parent function, $y = ax^2$ gives us the vertex (O,O), and it tells us to follow the pattern up 1, over 1, up 3 over 1, up 5 over one, and it keeps going up by 2. But when there is a stretch value that isn’t one then that pattern changes. If the a value is 2, for example, then you multiply the basic pattern by 2 so the pattern is up 2 over 1, up 6 over 1, up 10 over one, and so on. If the a value is, for example, 1/2 then you multiply the basic pattern by one half so it would be so that you go up 1/2 over 1 and so on.

Example:

So if the equation is: $y = 3(x-6)^2 +4$

That’s how a quadratic equation in the vertex form is graphed.

Week 7 – PreCalc 11

By aliessahv2016

On March 15, 2019

In Math 11

This week in Precalculus 11 we learned about discriminant. A discriminant is a part of the quadratic equation that helps us determine many things such as if the equation is factorable, how many roots it has, or if it has any roots at all before we actually solve the whole thing.

Example

Equation:

$3x^2 - 18x +27 = 0$

Step 1: make sure to take out anything common

$3(x^2 - 6 + 9)=0$

Step 2: determine what a, b, and c are.

a = 1

b = -6

c = 9

Step 3: fill the formula

$(-6)^2 - 4(1)(9)$

Step 4: simplify

$(-6)^2 - 4(1)(9)$

(36) – (36)

Explanation

Step 1: make sure to take out anything common

Taking out things that are common makes figuring out the answer a lot easier because the numbers are smaller to work with, but even if you leave everything in, it comes out with the same answer.

Step 2: determine what a, b, and c are

The formula for finding the discriminant relies on a, b, and c, and they are all in coordination with the equation. a would be equal to the first number (the number that has $x^2$ attached to it. b would be equal to the middle number (the number attached to x). c would be equal to the last number (the number that has no variable attached to it.). Writing out what a, b, and c are equal to makes it a less chance of error.

Step 3: fill the formula

Next, fill the formula according to coordination between letter and number

Step 4: simplify

There’s not much left to do except to find out the answer. The answer for this example was 0. This indicates that this equation has one real root. If the answer was any number bigger than 0 then that would mean that this equation has 2 real roots. If the answer was a number smaller than 0 (any negative number) then the equation has no real roots which means there is no need to solve the rest of the quadratic equation. That’s why it is helpful to find the discriminant, because we don’t need to solve more than we need to if we don’t need to.

Getting Through the Tough Times

By aliessahv2016

On March 14, 2019

In English 11

Read article here

The reason why this topic interested me is because of how I can relate to it. In this essay, the young author, Daniel, wrote about his struggle with sports. He has played pool his whole life and got so good that he made the most impossible shots. Except, one day out of nowhere, Daniel missed the simplest shot resulting in the loss of his momentum. From then on, his aim was off, his skill was minimal, and his power was gone. His continuous losses made him lose confidence leaving Daniel wanting to quit the sport he put many hours of his life into. Except instead of quitting, he practiced non-stop until he got his momentum back, in fact; he practiced until he was better than he was before. He started to win more games and make the shots he could before all while gaining the love he had for the sport he has played his whole life. The reason why his story resonates with me is because of a similar experience I went through. I started playing soccer when I was in elementary school and have worked hard since then to be where I am today, but it hasn’t been easy. It’s been tough on me not only physically, but mentally, too, experiencing countless moments where people that meant a lot to me didn’t believe in me. This made me lose immense amounts of confidence resulting in poor performance which made me want to stop playing soccer, but decided against it. I wasn’t going to let irrelevant people determine my fate in this game so, I went to the field any chance I got and trained hard until I perfected everything I could. As a result, I improved and proved all those people wrong by getting my skill better than it was before. I could have easily quit when things got hard, as could have this author, but we fought through it because we weren’t going to let a lack of confidence get it the way of letting go of something we love. That’s why I chose this article, because the experience the author described is something I have prominently struggled with, too.

What I enjoyed most about the author’s writing is how motivating it is. Hearing the author’s first line alone, “I believe that getting through the tough times will ultimately make us better,” is enough to motivate someone. Past the first line, too, the author continues to describe his experience with such encouraging words such as, “I realized moving past the hard times was the best thing I could’ve done. I could’ve just thrown in the towel and given up…but I knew that I could get through it.” These lines don’t even need to be in the context of just sports, it could be for anything. I loved how motivating this article was because it could not only help someone get through the same conflict the author and I overcame, but help anyone going through a tough time. This article could give some just an ounce of hope.

There are many movies I have watched and books I have read that have covered with someone at odds about the sport they love, much like the conflict the author described. There have also been movies, tv shows, and books about the same conflict, but not in sport scenario. It’s typically someone who has to overcome internal conflicts which is what this article is. The author lost his momentum in playing pool and felt the need to quit. I also experienced the same conflict where I told myself I couldn’t play soccer anymore when I was physically capable of doing so. It was just me telling myself I couldn’t. This is something that everyone in this world has to go though. Everyone’s conscious tells them they have to quit something when it gets hard, but it doesn’t have to end up that way. This article sums it up perfectly, “getting through tough times will ultimately make us better.”

Week 6 – PreCalc 11

By aliessahv2016

On March 9, 2019

In Math 11

This week in Pre-Calculus 11 we reviewed the different ways to factor, we learned how to find out what x can equal in a quadratic equation when we can factor it, and we learned how to find out what x can equal when a quadratic equation isn’t factorable. The ways we can do that is by completing the square or filling in the quadratic equation. The most difficult thing I think we learned is completing the square.

Completing the Square is a method used to solve a quadratic equation by changing the form of the equation so that one side is a perfect square trinomial. This makes the equation ‘kind of’ factorable and able to solve for x. Without the completing the square method, there would be no way to solve for x for a non factorable trinomial.

Example:

Explanation:

Step 1- find out if it’s a quadratic equation and if it’s factorable

To find out if it’s a quadratic equation, look for an exponent in the equation that has a degree of 2. To check if it’s factorable, multiply the coefficient attached to x2 and the number with no variable attached to it. In this case it would be 26. Now, I would check if two numbers that multiply two 26 also add up to the middle term then it’s factorable. In this case, the equation is non factorable, but it is quadratic.

Step 2- make sure x2 has a coefficient of one

If it doesn’t have a coefficient of one then make sure the number can be divided by the middle term. If it does, then divide the x2 coefficient and the middle term coefficient by the x2 coefficient to make it a 1.

Step 3- divide the middle term by 2 and square it.

At this point, we are at an equation that cannot be solved for x. We can make it solvable by completing the square. The middle term in this example is 6. So if we divide that by 2, which is 3, and square that, which is 9, then we just completed the square.

Step 4- add the # to the equation with a zero pair.

So if we add 9 to the equation (after the 6x), then we have to make it a zero pair by adding a negative 9. If we don’t add the negative 9 then the whole equation is changed, but adding a negative 9 makes a zero pair so it basically cancels each other out, but is very significant.

Step 5- multiply the 2 with the 9

After adding the zero pair, then brackets go around the first three terms. In this example it’s 2(x2 – 6x +9), and the negative 9 goes on the outside of it with the +13. In this case, the 2 on the outside of the bracket is multiplying the positive 9 that we added. To keep the zero pair we have to multiply the negative 9 by the 2 as well.

Step 6- factor and solve

The reason the brackets went around the terms before is because it factors perfectly into two factors that are exactly the same. Here it’s (x-3)(x-3). To put it in simpler terms its (x-3) squared. Now there’s not much left to do except to solve for x.

First move the -5 to the other side of the equal sign. Now to get rid of the two, divide both sides by it. Then to get rid of the square, square root both sides. When you add a square root sign to the fraction, you must put a ± sign before it because the outcome of the square root can be either a negative or a positive. Last, move the three over to the side with the fraction.

Step 7- don’t leave the denominator as a radical

As we learned last unit, radicals can’t be left in the denominator. So to get rid of it, multiply the top and bottom of the fraction by the square root of the denominator which is two. This makes only the top a radical now because the denominator will be equal square root of 4 which is 2.

Step 8- simplify where necessary.

This example didn’t need any because 10 can’t be broken broken down anymore.

Why Reading is Important

By aliessahv2016

On March 4, 2019

In English 11, Uncategorized

Read Article Here

The topic of the essay that I chose to write on was the enjoyment of reading. The reason why I chose this particular essay was because the author establishes that “reading lends the soul and mind a place to escape,” which is a quote that resonates with me. There have been countless times when I have been laying in bed sick, feeling down, or stressed out and all I did was pick up a book to make me feel a lot better. I agree when the author says that it’s a place for the mind and soul to escape because I have experienced it to go to another reality to escape my own reality. Another reason this essay interests me is because it suggests how “reading teaches us…giving you new words and expands vocabulary.” I also agree with this quote because everyday after kindergarten I would sit on my mom’s bed and read with her. Since then I have been a book junkie and I believe if I wasn’t, my vocabulary or even my writing skills wouldn’t be where they are today.

What I liked about the author’s style of writing is that is was persuasive without being too “in your face.” I didn’t feel as if I was being persuaded by the author that to like books is better, I just felt like I was reading someone’s great experience with reading. But in the end, I realized that it’s somewhat persuasive because it made me want to read a book. When she says she has had the benefit of “being a Bollywood sensation, a teenage spiritual medium,… a sexy southern waitress,…a witch with a price on her life,…and many more things,” it made me want to be all those things; to experience their emotions and live their lives, even if it is for a temporary amount of time.

The connection I made with the article I read was with the television show Gilmore Girls. The reason for this was because the daughter in the show, Rory, is a huge bookworm to a point where she has drawers upon drawers filled with book that she has read and has many more that she still has to read. There’s a particular quote in the series where she says that she “lives in two worlds; one is a world of books,” which, again, resonates with me along with relating to the article. The thing I noticed about the series, though, is that she tends to be the only one that likes to read. This also shows in her knowledge because out of everyone, she was definitely the smartest. But everyone around her seemed to be a few steps behind because reading isn’t big anymore. A reason people chose not to read, especially this generations group of teenagers, is because it comes off as lame. I don’t see how it could be, but it’s somewhat concerning. As I mentioned, I see reading as a chance to gain knowledge and seeing people read less and less is unsettling to think about let alone what’s going to happen in the future if we all just stopped reading . It keeps the mind active and without it, can have serious affects on our brains. Carl Sagan said, “One of the greatest gifts adults can give- to their offspring and to their society- is to read to children.” This proves that everyone reading can lead to a more knowledgeable society.

Week 5 – PreCalc 11

By aliessahv2016

On March 1, 2019

In Math 11

This week in PreCalc 11 we learned how to solve radical equations (which is an equation where the variable is under a radical). It was easy if we used our basic knowledge of equations; what we do to one side we do to the other (if I added 25 to one side I would add 25 to the other side of the equal sign) AND to cancel out an operation you do the opposite of it. (to cancel out -25 I would +25). With this basic knowledge it was pretty straight forward.

Example:

Explanation:

Step 1: apply the opposite operation to get rid of the square root

In the example, square roots were surrounding all the numbers in the equation so not much could be done without them gone. To get rid of the square roots you have to find the opposite operation which in this case will be to square everything. This is because once we square everything and it stays under the square root, the square root will cancel it out.

Step 2: bring like terms together

Now that the square root isn’t in the way of solving the equation we can do it now. First thing’s first, bring like terms together. The 5x and 2x are on opposite sides. So to remove the the 2x from the side it started on originally we have to subtract 2x to cancel it out. Then, since what we do on one side we do to the other, we have to add 2x to the other side. Now the -1 and 5 are on different sides of the equal sign so we have to +1 it started on originally and then +1 on the other side. After all the like terms are on the same side, combine them.

Step 3: SOLVE

All there really is to do is solve. To isolate x we have to divide by 3 and do that to the other side too. Then we are left with the answer which is 2.

Step 4:

Now that we know that x = 2 we need to verify our solution to make sure the root of the equation is a real root. For it to be a real root x has to be greater than or equal to 0. And once we have determined that, we have to put what x equals back into the original equation. In this case when I put 2 back into the original equation, both sides equal 3, therefore; 2 is a real root.

Week 4 – PreCalc 11

By aliessahv2016

On February 22, 2019

In Math 11

This week in PreCalc, we expanded on the ideas of radicals by learning how to add, subtract, multiply, and divide them. A lot of the ideas were straight forward, but the most challenging is dividing radicals.

Example:

Work:

Step 1: simply if necessary

Simplifying the given equation if it can be simplified makes the work easier later on because the numbers will be smaller.

Step 2: identify the conjugate

For dividing by a binomial, you have to multiply the numerator and the denominator by the denominators conjugate (is formed by changing the sign between two terms in a binomial). So the binomial in my example has a negative sign, but it’s conjugate will have a positive sign, and that’s the only difference between conjugates. The rest of the terms stay the same.

Step 3: multiply top and bottom by conjugate

Start with expanding the top and the bottom.

Step 5: simplify where necessary

After expanding, combine like terms, simplify radicals, and solve until you no longer can. When you can’t go any further, then you have reached your answer.

Week 3 – Precalc 11

By aliessahv2016

On February 14, 2019

In Math 11

This week in PreCalc 11, we learned about Absolute Values (of a real number, is the square root of the square root of a number. In simpler form, it’s the distance of a number on the number line from 0, and can only be a positive. So, the absolute value of -5 would be 5) and Roots/Radicals (a radical expression is defined as any expression containing a radical (√) symbol. It can be used to describe a cube root, a fourth root, or higher depending on the what the index is. The index is the number on the top left corner outside the radical symbol. A root is, when multiplied by itself is given a number. So, 2 is the root of 4 because 2×2=4)

The things we did were pretty straight forward this week, but the hardest thing I came across was evaluating expressions that had absolute values in them.

Example:

Explanation:

Step 1: find the absolute value first

I personally do this first because when the number you’re trying to figure out the absolute value for is a negative, then it turns into a positive so it’s easier to get that out of the way first. In this example, the value of a positive so we just keep it a positive

Step 2: finish the rest of the expression

The rest is simple BEDMAS, and trying to find the answer. Don’t forget, the math in the brackets should be done first, and then the rest follows.

Aliessah's Blog

My Riverside Rapid Digital Portfolio

Category: Grade 11 (Page 2 of 3)

Week 10 – PreCalc 11

Week 9 – PreCalc 11

Week 8 – PreCalc 11

Week 7 – PreCalc 11

Getting Through the Tough Times

Week 6 – PreCalc 11

Why Reading is Important

Week 5 – PreCalc 11

Week 4 – PreCalc 11

Week 3 – Precalc 11

Recent Posts

Categories

Archives