I learned a bunch of new concepts pertaining to radicals this unit, as I look back on this unit I want to remember when to use what rules when specifically(like remembering that you cant find the square root of a negative number) I think it will help me to understand it better too in the long run. Radicals can be compared to fractions in that they can only be added or subtracted if certain things match (sort of like the denomenator) your radicand and index must match.I even learned more about myself this unit, I learned that I need to ask more about my homework until I truly understand and can do the questions fully on my own. I need to pay more attention to extra practice to have to do rather then assuming that I already know how to do all forms of questions (when I didn’t). I also learned that just because you do really good on one unit doesn’t necessarily mean I’ll do good on all of them, and I have to be more consistent.
If I could go back and change anything about my math 10 experience I would tell myself these things:
- Do your homework, because it helps you remember everything so much easier.
- Go to tutorials if you don’t get anything even if its just the simplest thing its worth it to figure it out rather then not asking.
- Start studying for the midterm farther ahead, I left this until last minute and it showed in my test score and if I could back I would change it.
- Do your blogposts every week, because otherwise you are going to have like 4 to do at once and its much harder to do then just sticking to 1 every week.
- When studying practice it by writing and trying equations, it helps you to remember it better.
Using the equation y=mx+b we can solve for a (straight) line. When using this equation you plug things in and then you add your co-ordinates to make your equation fully solved. When using this equation it can be tricky to know which variables stand for what (plug-ins) but after practicing it will just come naturally. M stands for the slope so the rise/run between to points on a graph (that are on your line) and b stands for your y intercept, but don’t be fooled it can be negative OR positive depending on the line you are dealing with. Once you have those two you solve for the other then you plug in two of your co-ordinates to evaluate for the rest of the line.
For example a line that passes through the point (0,2) <on the y axis x=0 so it is an intercept> with a slope of 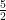
In the photo below I have shown you how this would look on a graph and how you would be able to find it using the information given. 
What we learned this week builds on my last blogpost as this one uses the last method within it. Last week we would used a different function (y) it can be mixed up so pay attention, to represent the outputs and range of the relation, but in this week we use f(x)= to represent the function instead. To use function you basically just input your numerical x value anywhere in the equation where x is already then you solve. Using function notation you can find lines and unknown co-ordinates because of the input abilities. Down below I have shown you how to use function notation to input plots on a graph, and the difference between function notation and x-y notation.

This week we learned about functions. Functions are related to domain and range because they are what make it up (relates them through an equation). You use it by using the replacement for x and y in equations to find the opposite. It can be tricky though to spot this special type of relation because each element of the domain is related to exactly one element of the range, which can be hard to spot sometimes. Im going to show you all the methods you can use to spot what relations are real functions. First you can see using an arrow diagram, the rule is if more than one arrow leaving an input number to an output means it is not a function, then ordered pairs, if the input value (x,y) shows up more than once in your sequence then it isn’t a function, and lastly in graphs you can find out whether it is a function by using the vertical line method, using this method you can find a “fake” function by seeing if any vertical line drawn on the graph intersects more than once on the graph then it is not a function. Down below I have shown you examples of spotted non-functions and real ones.

This is a change up to the math we’ve been dealing with recently as it offers a way more visual component to it. It taught me how to further deal with expressions through input and output (putting numbers into a variable to see a different outcome). It is a skill that can be used in things like graphing etc. and using input and output methods using graphs, ordered pairs, table of values, and mapping diagrams which overall just show the relation between the independent and dependent variables. Below I have showed you what the different methods look like, as they’re plenty to choose from which can make it easier to find which one is best suited for you, makes the most sense.

Throughout all the chapters we have learned so far many connections can be found that can be used to create memorization techniques. I have chosen to show you the connection I made between GCF and LCM and the polynomial unit we just recently looked at. Looking at knowledge from previous units that we are able to place on the next really allows for deeper understanding of a topic. In the most recent unit we studied (polynomials) I came across factoring, which I found decently easy when it came to the basics but then we go to further factoring with larger numbers and it started to confuse me, as it just looked to be to much. Then I started to look at it using a different perspective which really allowed me to understand it, once I started being able to see that I only needed to find the greatest common factor between these numbers is what really made it clear. Below I have shown you an example; which although make look very large (number wise) can actually be very small (using GCF).

When factoring trinomials you can use multiple methods like the inspection method, but this method I’m going to show you is using algebra tiles, which helps for those who are more visual learners. It can be difficult sometimes to figure out how to sort the tiles so they make a perfect square, but with practice, and trial and error you will get better at figuring out how to assort them quicker. First you need to know what each tile is equal to so in my diagram below I have shown you which one is equal to which. To factor a trinomial you are basically just breaking down the equation, with this method you are given the tiles but it’s up to you to sort them properly.

Last week I explained how to multiply binomials, but now we will be multiplying with trinomials, with a larger amount of terms this can start to become confusing using FOIL, so I will show you how to break it down step by step. This has a few steps that you have to follow, however if you want to get the right answer its best to follow them at first, at least until you get the hang of the shortcuts. I have given you an example of an equation down below and I have gone through what all the steps in the photo. First you will FOIL but on each side of the subtraction side, making sure all the numbers get factored with each other once, next you will you will combine like terms then you will multiply by the original co-efficient and the combine like terms again (terms with the same variables) then you will combine both halves of the equation.
4(a-4)(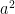 -3a-6)-(4a-3)(4a+3)
-3a-6)-(4a-3)(4a+3)










