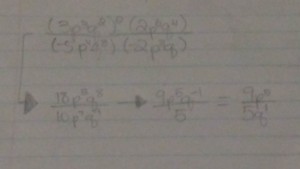Represent Repeated Multiplication with Exponents
Representing repeated multiplication with exponents isn’t that hard. All you need to do is count how many of the numbers are and then put the number as a power. Here is an example- 5•5•5•5•5= 5⁵
So the question was multiplying five, five times in a row, but then you could simplify it to 5⁵.
How Powers Represent Repeated Multiplication
Exponents (powers) represent how many times a number is multiplying itself. So instead of writing on forever like 2•2•2•2•2•2•2•2•2•2•2•2•2•2•2•2•2•2•2•2, you could simplify that to 2²⁰. Using powers is a more simple way of writing out long multiplications. At the end, 2•2•2= 2³, meaning that if 2•2•2= 8 that should mean that 2³= 8 to because at the end they are the same question.
2³ and 3² with Models
math-everything-i-know-about-exponents-aileen-klassen
⬆Click Link for Video!⬆
The difference between 2³ and 3²
If you look at 2³ and 3² you might think that they would equal the same thing because in multiplication, when you flip the numbers around, it should equal the same thing. A common mistake is to do: 2•3=6 and 3•2=6. But it’s actually supposed to be 2•2•2=8 and 3•3=9. As you can see, the numbers are different. You can’t use short cuts like 3•2 because that isn’t the right answer. The exponent is supposed to represent how many times the base will multiply by itself. So 2³ would be 2(Base) multiplied by itself 3(Exponent) times, and that is how you would get 2•2•2=8.
Evaluating Powers with Integral Bases and Whole Number Exponents
Having integral bases doesn’t change the way you do the math. The exponent still means how many times that you multiply the number. The only difference if that if the exponent is an even number, the answer will be positive. If the exponent is an odd number, it will be negative. Here is an example: = 25 and
= -125. Because since you know that a negative multiplied by a negative equals positive and a positive multiplied by a negative equals negative, it makes sense that a negative base to the power of a positive number will equal positive. Repeated multiplication example: (-5)•(-5)•(-5)•(-5)= 625⬅ Positive because it was multiplied and even amount of times. (-5)•(-5)•(-5)= -125⬅Negative because it was multiplied an odd number of times. It become negative because (-5)•(-5) equals
, then multiplying it by a negative again will make the answer
because you multiplied the positive answer, (-5)•(-5) and then added a third negative number (-5)•(-5)•(-5) making the answer negative. Here is a step by step: (-5)•(-5)•(-5)= 25•(-5)=
.
The Role of Parentheses (Brackets) in Powers
If you were to be given the questions (-2)⁴, (-2⁴) and -2⁴ you would get different answers. Even though you would get the same answer with -2⁴ and (-2⁴), writing them out in a repeated multiplication would look different. For (-2)⁴, writing it out as a repeating multiplication would look like this: (-2)•(-2)•(-2)•(-2)= 16 and writing out (-2⁴) would look like this: (-1•2•2•2•2)= -16. You get the same answers but the writing them out part is different. Because in (-2⁴), the exponent is in the brackets meaning that everything happens inside the brackets. But for (-2)⁴ it is whatever is in the brackets four times. Now for -2⁴. When you are doing this, the is a coefficient. So it represents
. You would use BEDMAS for this one, so you would do 2⁴ which equals 16, then you would do (-1)•16= -16. So the answer would be -16, which is very different from 16, so don’t mix it up!
Exponent Laws for Multiplying and Dividing Powers with the same Base
When you get a question like 2³÷2², you don’t need to use BEDMAS to find the answer. There is a simpler way you can do that. Since it is division, you can subtract the exponents so you would have = 2¹= 2. For multiplication, you would add the exponents instead of subtracting them: 2³•2²=
= 2⁵= 32. So if the bases are the same you can simplify it by; Multiplication~Adding the exponents or Division~Subtracting the exponents.
Exponent Law for Raising a Product and Quotient to an Exponent
Like in the last question, for multiplication (Product Law) you would add your exponents to get a single power if the bases are the same, and for division (Quotient Law) you would subtract your exponents to get a single power if your bases are the same.
The Law for Powers with the Exponent Zero
If you think back to multiplication, you would think that 5⁰ would equal 0. But that is wrong, 5⁰=1. Here is why; with powers there is a pattern, each time the exponent goes up by one, the answer multiplies by the base, and when the exponent goes down by one, the answer divides by the base. Here is an example: 5⁵= 3125➡ 5⁴=625➡ 5³=125➡ 5²=25➡ 5¹=5 and if the pattern continues to 5⁰, that should mean that 5⁰=1 because 5÷5=1. Also if you use the quotient rule for 5²÷5² and use BEDMAS, it would be: 25÷25=1 so that would mean that = 5⁰=1 because it is the answer to the same question. That justifies that x⁰ will always equal 1.
Using Patterns to Prove that bases with the Exponent 0 Equals 1
Like I had explained before, the pattern is that each time the exponent rises by 1, your answer will by x times bigger than the the one before it (x as a base). So that should mean that it works the same going down, then you divide the answer by x each time the exponent goes down by one, meaning that x⁰=1.
Law for Powers with Negative Exponents
With negative exponents, you need to be able to flip the number so it’s in a fraction. Let’s use . So right now we can put it in the fraction form:
. Now we flip it to
. Now since it’s positive, we can use BEDMAS to solve it. So 2⁵= 32. So now we have
. You can leave it like that or you can solve it. So 1÷32= 0.03125. So whenever you need have a negative exponent, you need to turn it into fraction form if it is not already and then you switch the numbers with the exponents that are negative from the top to the bottom and vice versa.
Patterns for the Negative Exponent Law
The pattern for negative exponents are the same pattern as positive exponents, the only difference is that it’s a fraction with 1 as a numerator. So here is an example of the pattern: 2³=8➡ 2²=4➡ 2¹=2➡ 2⁰= 1➡ =
➡
=
➡
=
. So the pattern continues, but instead as a fraction instead of a whole number.
Applying Exponent Laws to Integral and Variable Bases
For Variable Bases-
x⁸=x⁸ You can’t change it because you don’t know what x equals
y⁰= 1 because you know no matter what number, that ANYTHING to the power of 0 will equal one.
For Integral Bases-
They work the same as positive bases, just that you have to beware that if it’s to an uneven power, it will be negative, it it is even the answer will be positive.
Identifying an Error in a Simplification of an Expression Involving Powers
If you see something like 3(2³) some people might doing something like = 6³. THAT IS WRONG.
You need to stick to the rules of BEDMAS and do the exponents first, so you should do- 2³=8= 3•8=24. So 3(2³)= 24.
Using the Order of Operations on Expressions with Powers
For example you could use 5(2³). So because of BEDMAS, you have to do do the exponent first by doing 2³ which equals 8. Then you will end up with 5(8) and now you just need to multiply 5•8=40. So the answer to 5(2³)= 40.
Determine the Sum and the Difference of Two Powers
All you need to do is BEDMAS to calculate the Sum and the Difference.
Ex: 5²+2³= 25+8= 33
5²-2³= 25-8=17
Identifying an Error in Applying the Order of Operations in an Incorrect Solution
This is wrong:
5²+5=
10²= 100
So you would have to do the exponents first and then you could do the addition second.
Correct way:
5²+5=
25+5= 30
So you can see if you do it the wrong way, you can get completely different numbers. In the examples you could have gotten 30 or 100.
Using Powers to Solve Measurement Problems
For example, if you need to find the grey part of the square. You can see that there is a white square  inside the grey square, meaning that you want to take out the area of the white square. So first, you will need to calculate the area of the the grey part: 5cm²= 25cm². Now you can calculate the area of the white square: 1cm²= 1cm². So now you can subtract the area of the white square from the area of the grey square: 25cm²-1cm²= 24cm². So that means that the area of the grey space is 24cm²
inside the grey square, meaning that you want to take out the area of the white square. So first, you will need to calculate the area of the the grey part: 5cm²= 25cm². Now you can calculate the area of the white square: 1cm²= 1cm². So now you can subtract the area of the white square from the area of the grey square: 25cm²-1cm²= 24cm². So that means that the area of the grey space is 24cm²
Using Powers to Solve Growth Problems
Using exponents can be helpful for growth problems. For example, two bacteria are in a jar, each hour they double. So you could use 2² for the first hour, then it would be 4², 8², 16²… So it can show how it duplicates every hour and you would be able to figure out how many bacteria are in the jar. It makes figuring out the answer a lot easier and faster. It also helps you understand the question more when you think of it with powers.
Order Of Operations on Expressions with Powers Involving Negative Exponents and Variable Bases
All you need to remember is all of the laws and keep BEDMAS in mind: